Notes on Machine Learning 13: Graphical Models
by 장승환
(ML 13.1) (ML 13.2) Directed graphical models - introductory examples
(Directed) Graphica “Models” aka “Bayesian” networks
Better name would be “conditional independence diagrams” of probability distributions
Key notions:
- factorization of probability distributions
- notational device
- useful for visualization of
(a) conditional independence properties
(b) inference algorithms (DP, MCMC)
Why conditional independence important? Tractable inference
Thnking “Graphically”
Let $A, B, C$ be random variables.
$p(a, b,c) = p(c\vert a, b)p(a, b) = p(c\vert a, b)p(b\vert a)p(a)$
If $B$ and $C$ are independent given $A$, then $p(c\vert a, b) = p(c\vert a)$.
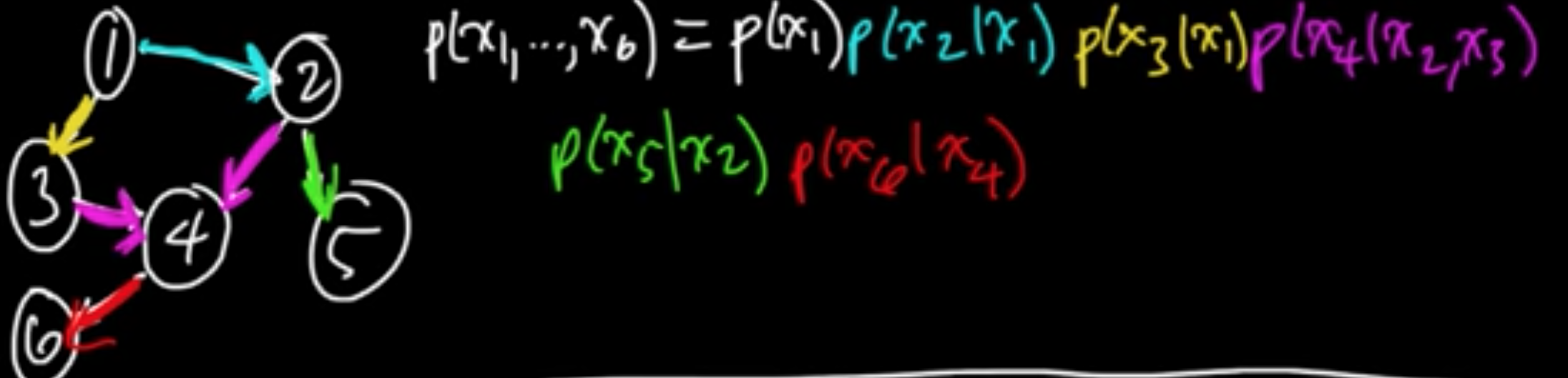
(ML 13.3) (ML 13.4) Directed graphical models - formalism
Notation.
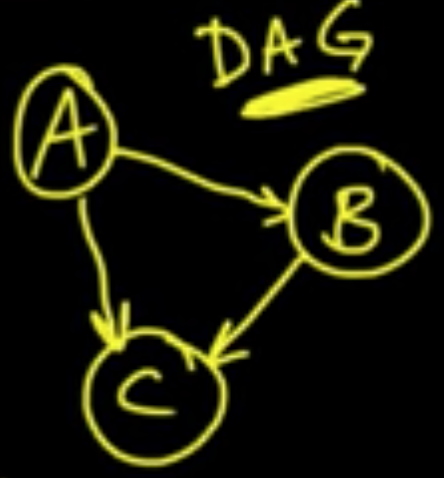
- DAG (Directed Acyclic Graph) : no directed cycles
- $pa(i) =$ parents of vertex
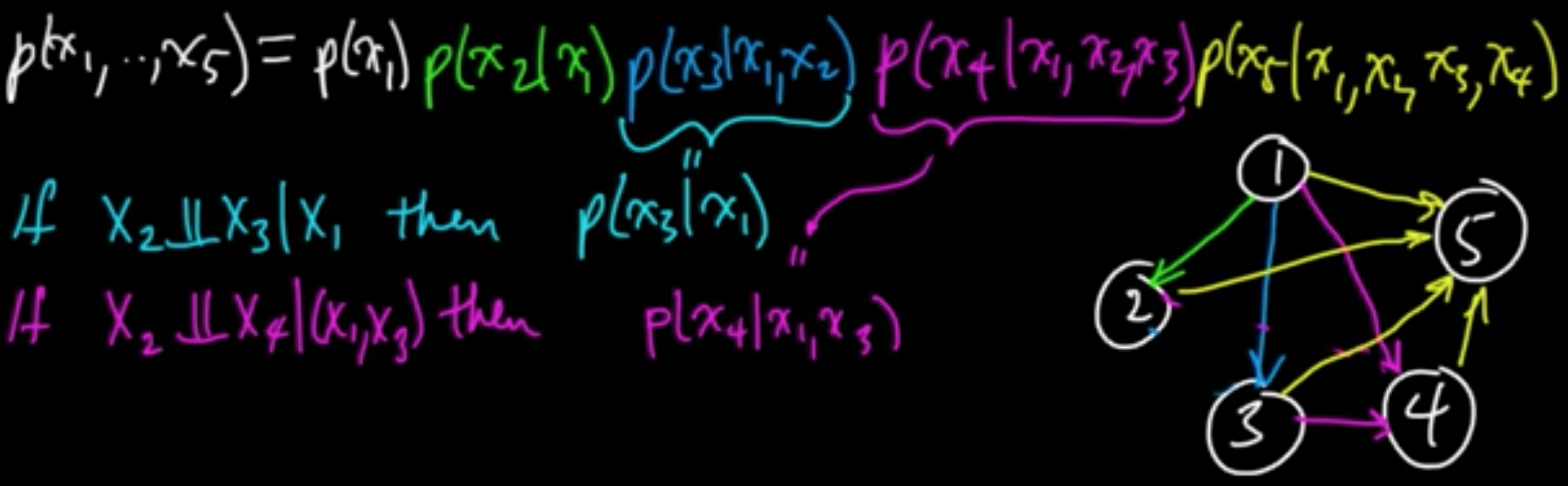
Definition. Given $(X_1, \ldots, X_n) \sim p$ (pmf or odf) and an ordered DAG $G$ on $n$ vertices, we say $X$ respects $G$ (or $p$ respects $G$) if
Remark. This does not imply that any particular random variables are conditionally dependent.
Example. $X = (X_1, X_2, X_3)$ mutually independent
Then $p(x_1, x_2, x_3) = p(x_1)p(x_2)p(x_3)$
Terminology. A Complete directed graph.
Example. Any distribution respects any complete DAG.
Remark.
- Can combine random variables into vectors
- If the factors are normalized conditional distributions, then the product is normalized also. (Exercise)
(ML 13.5) Generative process specification (“a handy convention”)
$X_1, X_2 \sim \text{Bernoulli}(1/2)$, independent
$X_3 \sim N(X_1 + X_2, \sigma^2)$
$X_4 \sim N(aX_2 + b, 1)$
$X = (X_1, \ldots, X_5)$ respects the following graph
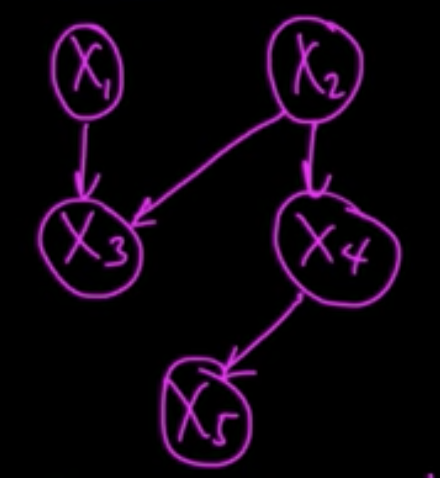
and wee have the following factorization $p(x_1, \ldots, x_5) = p(x_1)p(x_2)p(x_3\vert x_1, x_2)p(x_4\vert x_2)p(x_5\vert x_4)$.
Nice sampleing and visualization.
Examples of (Directed) Graphical Models
(ML 13.6) Graphical model for Bayesian linear regression
$D = ((x_1, y_1), \ldots, (x_n, y_n)), x_i \in \mathbb{R}^d, y_i \in \mathbb{R}$
$f(x) = w^T\varphi(x)$
$w \sim N(0, \sigma_0^2I)$
$Y_i \sim N(w^T\varphi(x_i), \sigma^2)$, independent given $w$
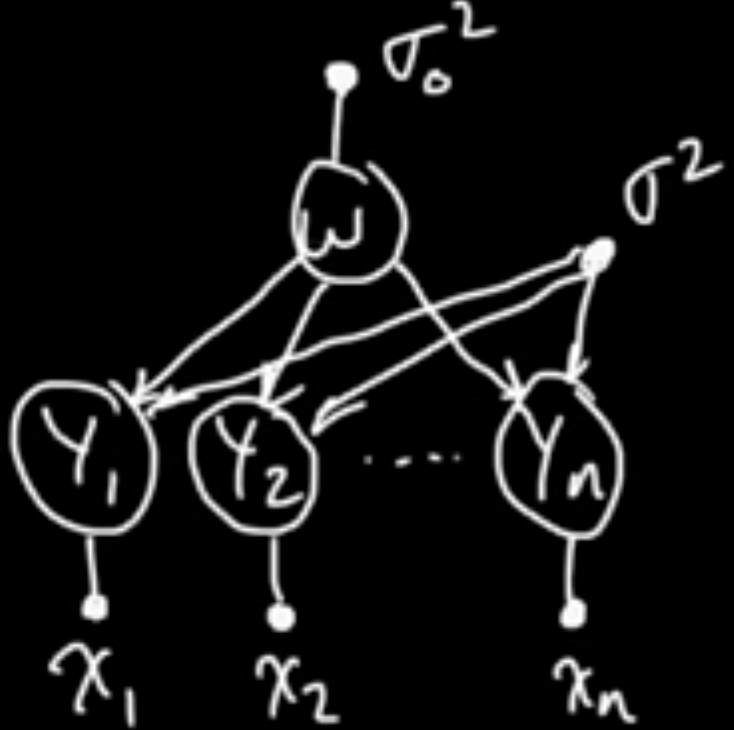
$p(w, y_1, \ldots, y_n) = p(w)\prod_{i=1}^n p(y_i\vert w)$
Plate notation.
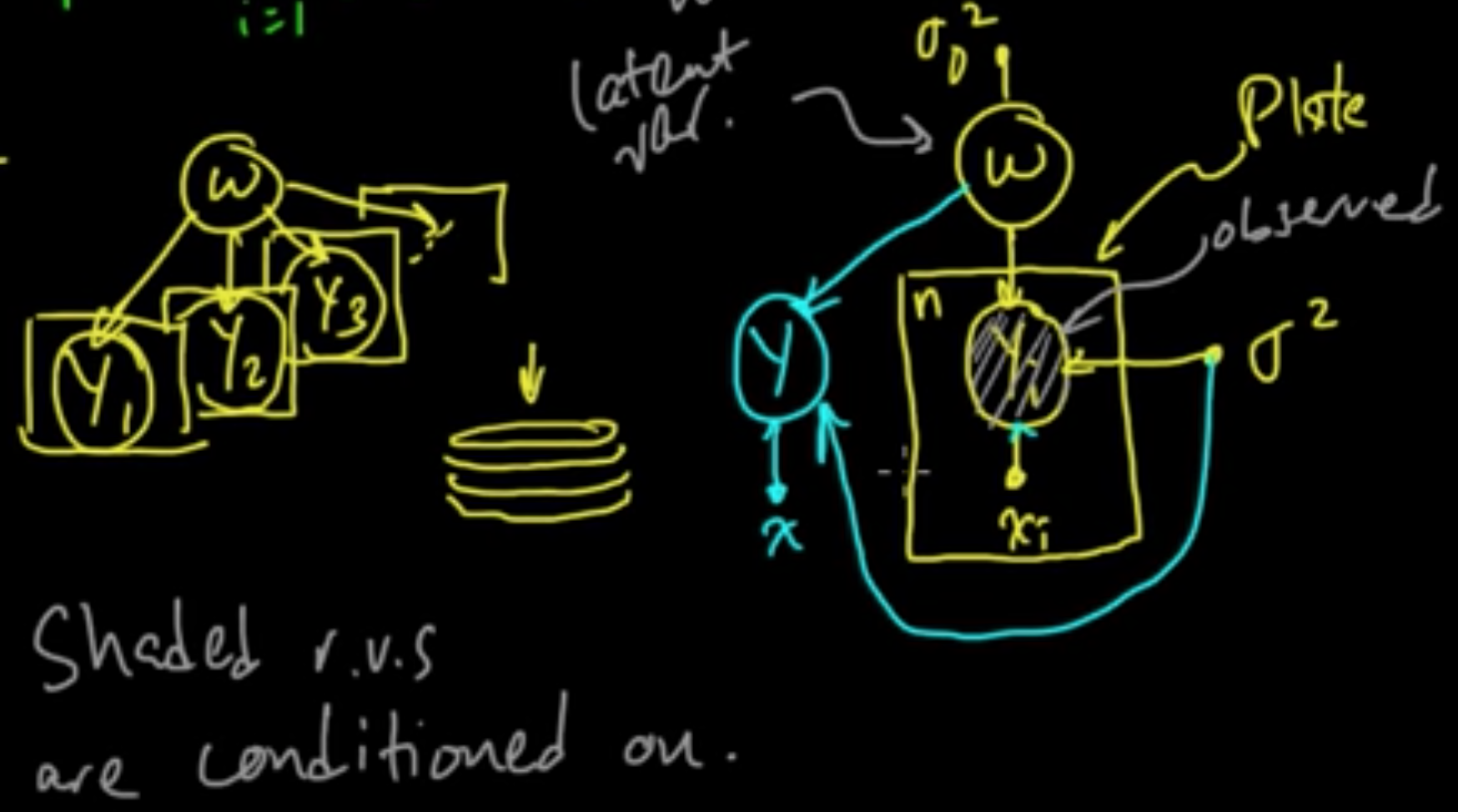
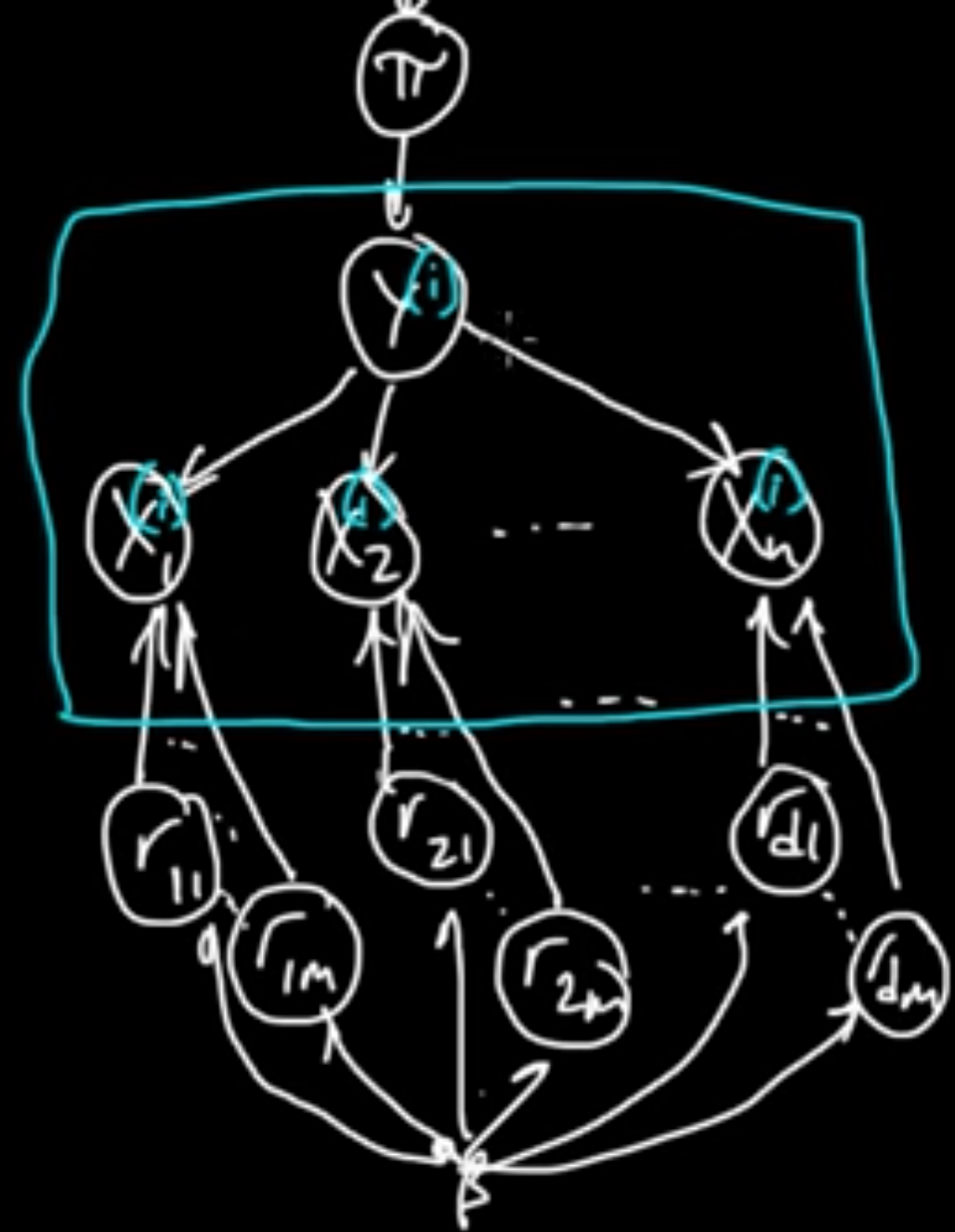
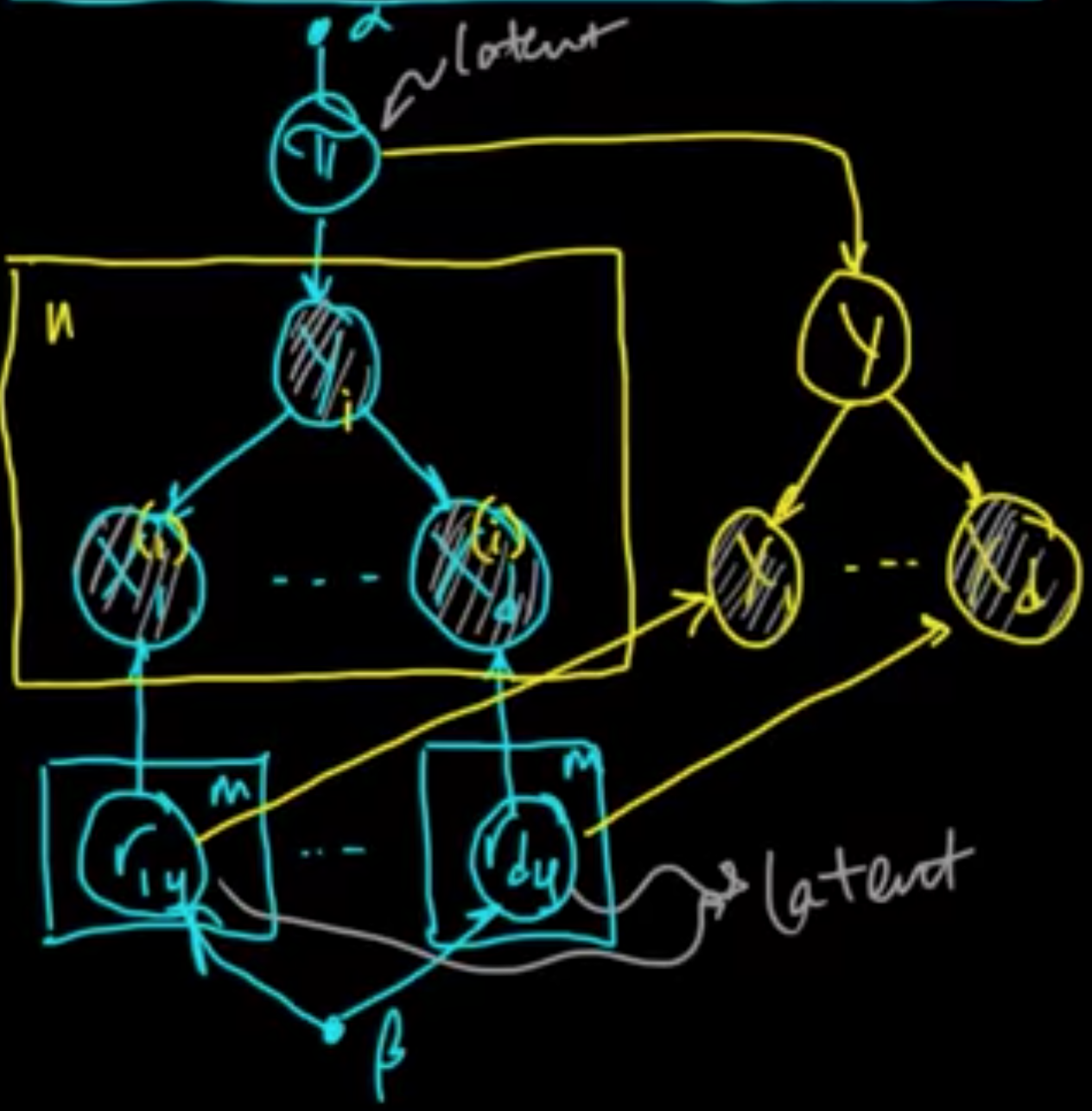
(ML 13.7) Graphical model for Bayesian Naive Bayes
$D = ((x^{(1)}, y_1), \ldots, (x^{(n)}, y_n)), x^{(i)} \in \mathbb{R}^d, y_i \in \{1, \ldots, m\}$
$\pi \sim \text{Dir}(\alpha)$
$r_{jy} \sim \text{Dir}(\beta)$ for $j = \{1, \ldots, d\}, y \in \{1, \ldots, m\}$
$Y \sim \pi, Y_i \sim \pi$
$X_j \sim r_{jY}, X_j^{(i)} \sim r_{jY_i}$
(ML 13.8) (ML 13.9) Conditional independence in (directed) graphical models - basic examples
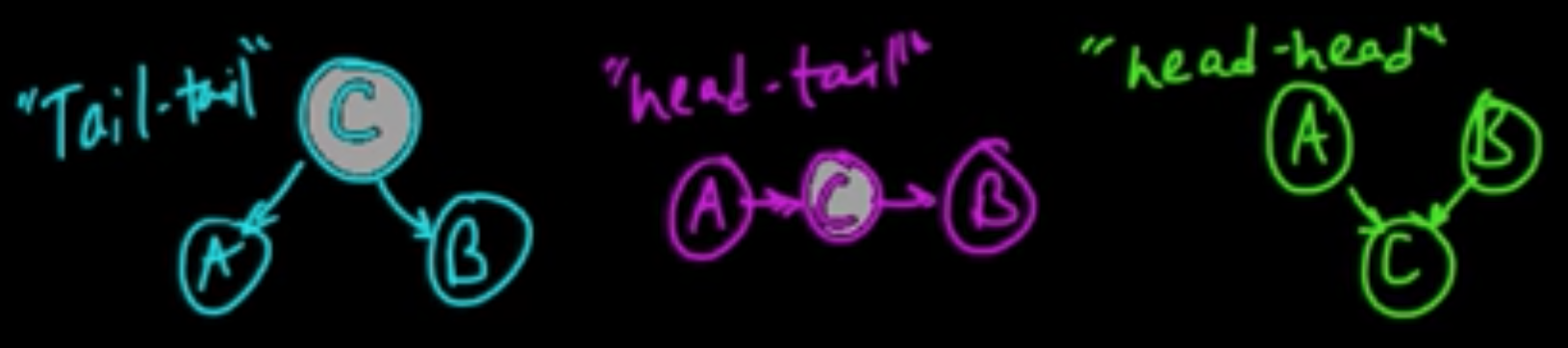
1 “Tail-tail”
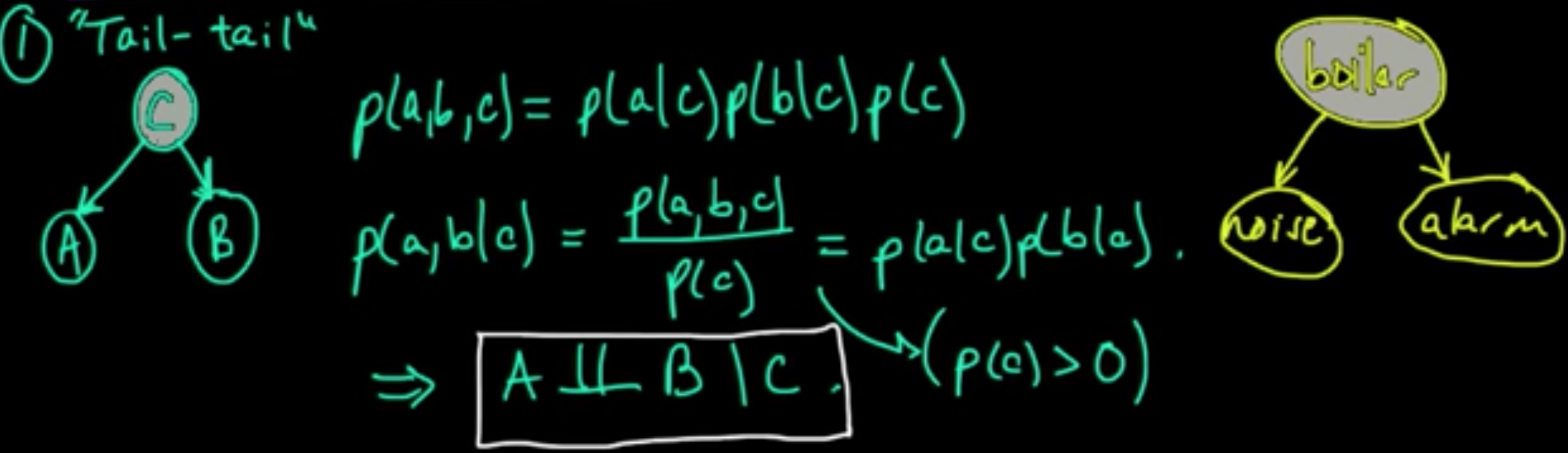
2 “Head-tail” (or “Tail-head”)

3 “Head-head”

(ML 13.10) (ML 13.11) D-separation
“The whole point of graphical models is to express the conditional independence properties of a probability distribution. And the D-separation criterion gives you a way to read off those conditional independence properties from the graphocal model for a probability distribution.”
D-separation is a vast generalization of these:
Terminology. Descendents
Let $G$ be a DAG. Let $A, B, C$ be disjoint subsets of vertices.
($A \cup B \cup C$ is not necessarily all of the vertices.)
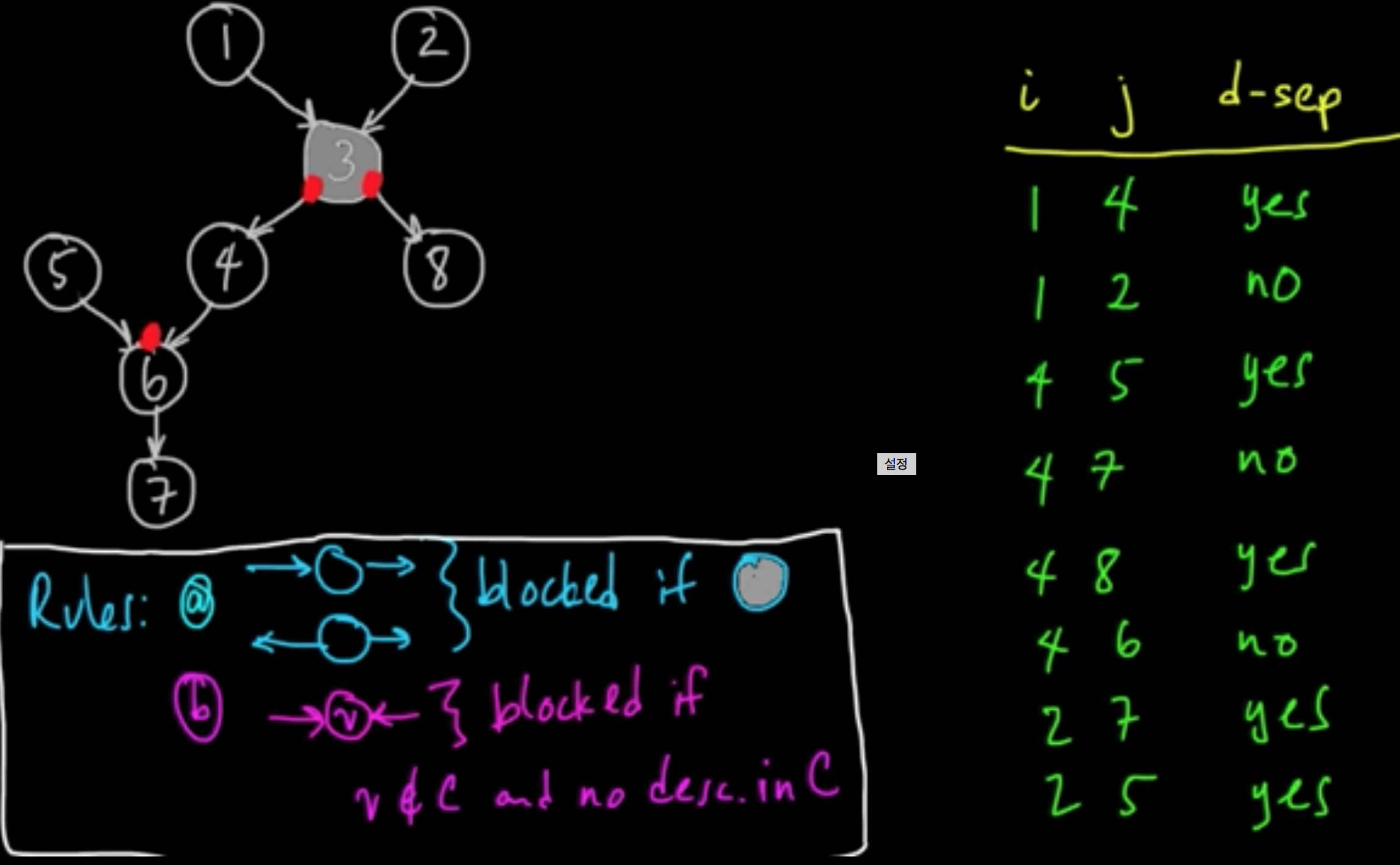
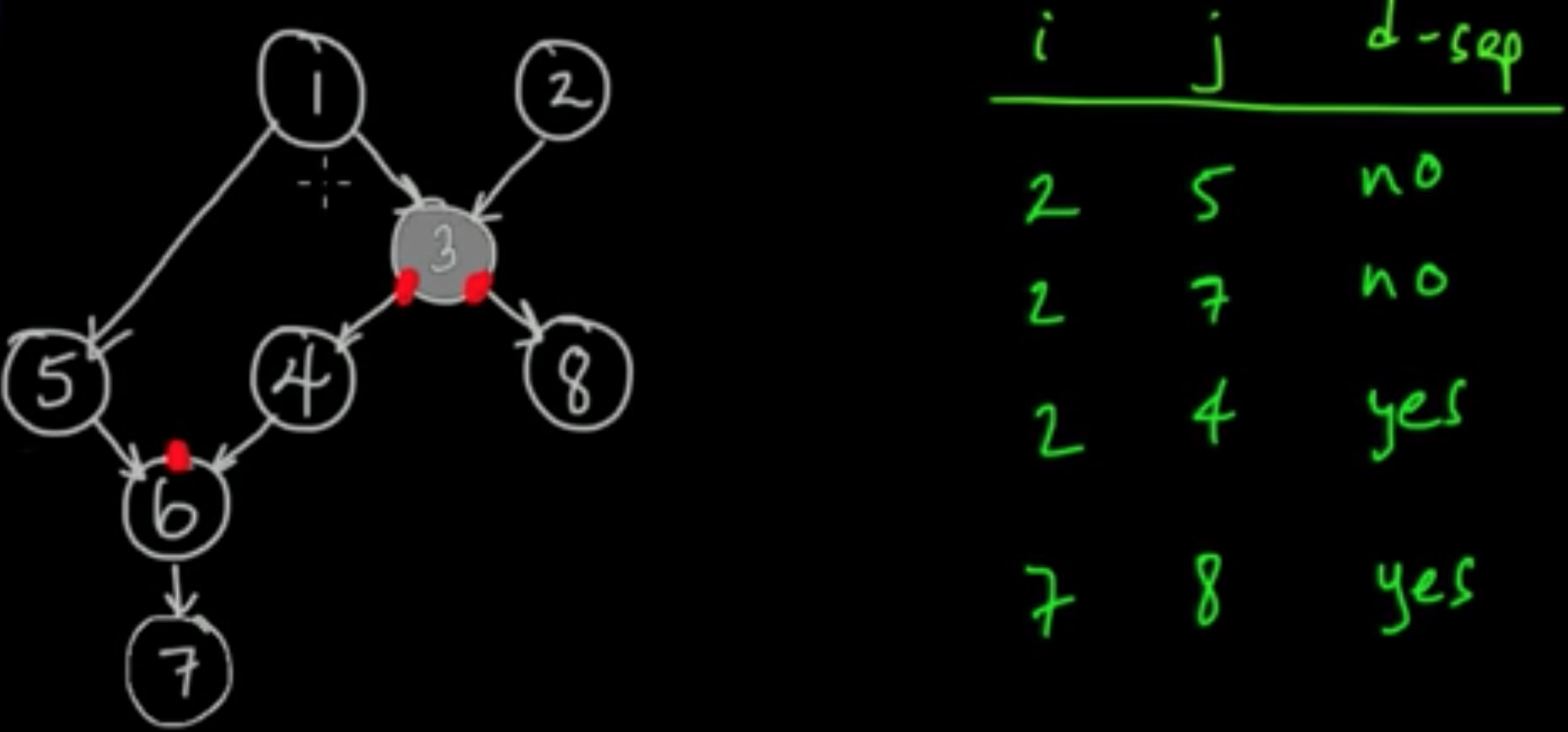
Definition. A path (not necessarily directed) between two vertices is blocked (w.r.t. $C$) if it passes through a vertex $v$ s.t. either (a) the arrows are head-tail or tail-tail, and $v \in C$ or (b) the arrows are head-head and $v \not\in C$ and none of the descendents of $v$ are in $C$.
Definition. $A$ and $B$ are d-separated by $C$ if all paths from a vertex of $A$ to a vertex of $B$ are blocked (w.r.t. $C$).
Theorem (d-separation). If $A$ and $B$ are d-separated by $C$ then $A$ and $B$ are conditionally independent given $C$.
(ML 13.12) (ML 13.13) How to use D-separation - illustrative examples
Example 1. $C = \{3\}$ Are $X_i$ and $X_j$ independent given $X_3$?
Example 2.

Example 3.
Subscribe via RSS
