Notes on Machine Learning 11: Estimators
by 장승환
(ML 11.1) Estimators
Model the data as random variables: $D = (X_1, \ldots, X_n)$.
Definition. A statistic is a random variable $S = f(D)$ that is a function of the data $D$.
Terminology. An estimator is a statistic intended to approximate a parameter governing the distribution of $D$.
Notation.
- $\hat{\theta}$ denotes an estimator for a parameter $\theta$.
- $\hat{\theta}_n$ emphasize (the dependence on) $n$
Example. $X_1, \ldots, X_n \sim N(\mu, \sigma^2)$, iid
- Sample mean: $\,\,$ $\hat{\mu} = \bar{X} = \frac{1}{n}\sum_{i=1}^nX_i$ $\,\,$ /cf. $\sigma^2 = \mathbb{E}((X - \mu)^2)$
- “Biased” sample variance: $\,\,$ $\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n(X_i -\bar{X})^2$
- “unbiased” sample variance: $\,\,$ $s^2 = \frac{1}{n-1}\sum_{i=1}^n(X_i -\bar{X})^2$
Definition.
- The bias of an estimator $\hat{\theta}$ is $\,$ ${\rm bias}(\hat{\theta}) = \mathbb{E}(\hat{\theta}) - \theta$.
- An estimator $\hat{\theta}$ is unbiased if $\,$ ${\rm bias}(\hat{\theta}) = 0$.
Example.
- $\hat{\mu}$ is unbiased: $\mathbb{E}(\hat{\mu}) = \mathbb{E}(\frac{1}{n}\sum_{i=1}^nX_i) =\frac{1}{n}\sum \mathbb{E}(X_i) = \frac{1}{n}\sum \mu = \mu$
- $\hat{\sigma}^2$ is biased. (Exercise)
- $s^2$ is unbiased. (Exercise)
(ML 11.2) Decision theory terminology in different contexts
| General | Estimators | $^*$Regression/Classification (SL) |
| Decision rule $\delta$ | $^*$Estimator function $g$ | Prediction function $f$ |
| State $s$ (unknown) | Parameter $\theta$ (unknown) | Target value $Y$ (unknown) |
| $^*$Data $D$ (observed) | Data $D$ (observed) | Point $X$ (observed) |
| Action $a = \delta(D)$ | Estimator/Estimate $\hat{\theta}=g(D)$ | Prediction $\hat{Y} = f(X)$ |
| Loss $L(s, a)$ | Loss $L(\theta, \hat{\theta})$ | Loss $L(Y, \hat{Y})$ |
Example. (Estimators)
An estimator is a random rariable: $\hat{\mu} = \frac{1}{n} \sum_{i=1}^n X_i$.
An estimate is a number: $\hat{\mu} = \frac{1}{n} \sum_{i=1}^n x_i = 2.3$.
(In some situation, the procedure $g$ is refered to as an estimator!)
(ML 11.3) Frequentist risk, Bayesian expected loss, and Bayes risk
Loss and Risk. Exciting session to clear up all the mud!
Data: $\,$ $D = (X_1, \ldots, X_n)$, $D \sim p_\theta$
Parameter: $\,$ $\theta \sim \pi$ $\,$, i.e., the parameter $\theta$ is a random variable.
Estimator: $\,$ $\hat{\theta} = f(D) = \delta(D)$
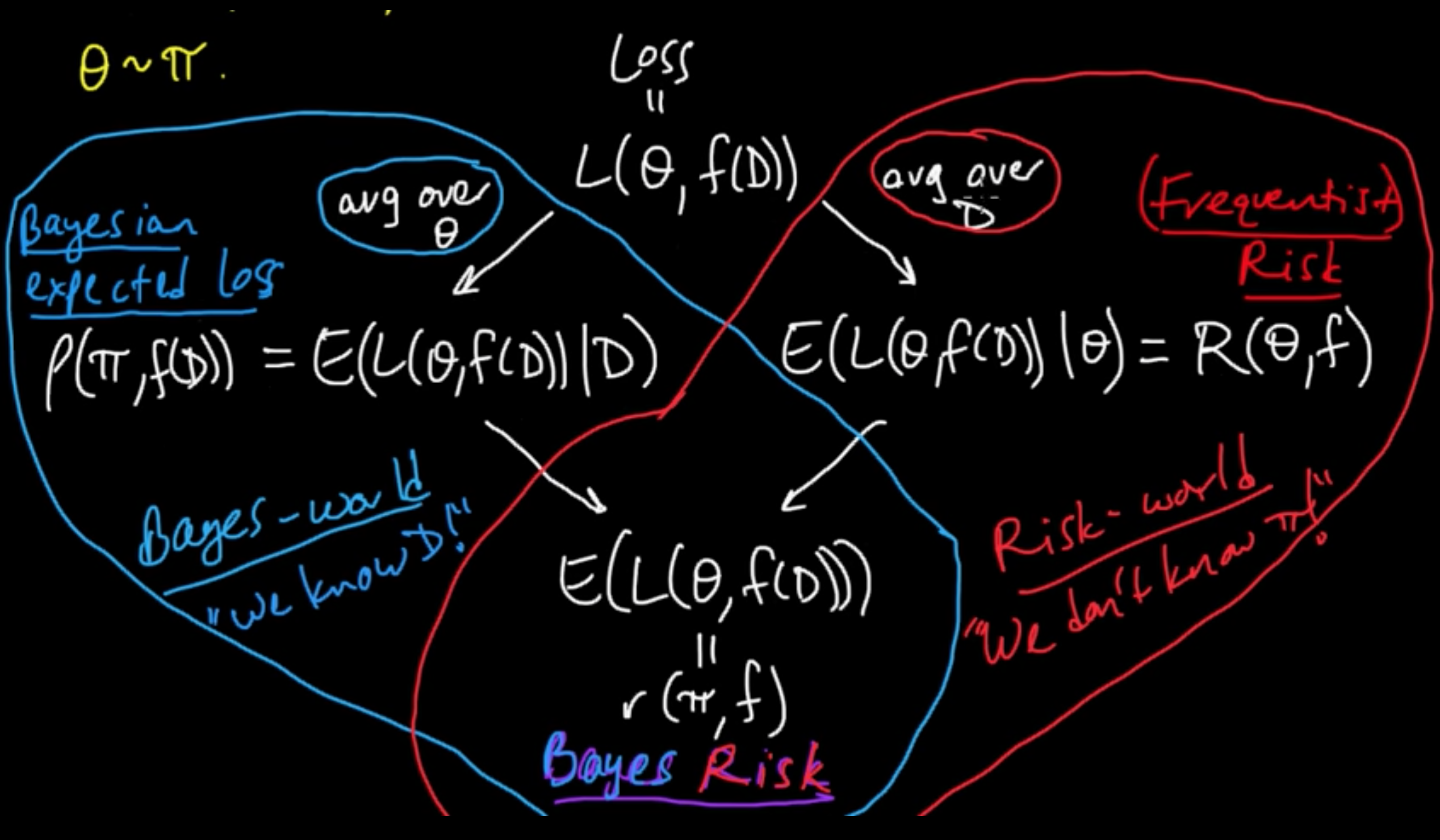
Everything begins with : $\,\,\,\,\,$ Loss $=L(\theta, f(D))$.
We wanna minimize the loss but it’s an RV!
Two option to deal with it:
- Averaging over $\theta$ given the data : $E(L(\theta, f(D)) \vert D) =:\rho(\pi, f(D))$ Bayesian expected loss
- Averaging over the data given $\theta$ : $E(L(\theta, f(D)) \vert \theta) =: R(\theta, f)$ (Frequentist) risk
(ML 11.4) Choosing a decision rule - Bayesian and frequentist
How to choose $f$.
Bayesian: Assume $\pi$
Case 1. Know $D$. Choose $f(D)$ to minimize $\rho(\pi, f(D))$
Case 2. Don’t know $D$. Choose $f$ to minimize $r(\pi, f)$
Frequentist: Introduce a furthere principle to guide your choice.
(a) Unbiasedness
(b) Admissibility
(c) Minimax
(d) Invariance
(ML 11.5) Bias-Variance decomposition (MSE $=$ bias$^2$ + var)
“A super impportant port of ML is what’s called model selection and a tool for model selection is the bias-variance decomposition.”
Almost trivial identity but extremely handy.
Definition. Let $D$ be random data. The MSE of an estimator $\hat{\theta} = f(D)$ for $\theta$ is
Put $\vert \theta$ to emphasize we’re not averaging over $\theta$ here (we don’t have a distribution over $\theta$).
We’re averaging over the data!
${\rm MSE}(\theta)$ is nothing but the risk $R(\theta, f(D))$ under square loss, i.e., when the loss function is the square of the deifference.
Recall. ${\rm bias}(\hat{\theta}) = \mathbb{E}(\theta) -\theta$.
Proposition. MSE$(\theta) = {\rm bias}(\hat{\theta})^2 + {\rm var}(\hat{\theta})$
Proof:
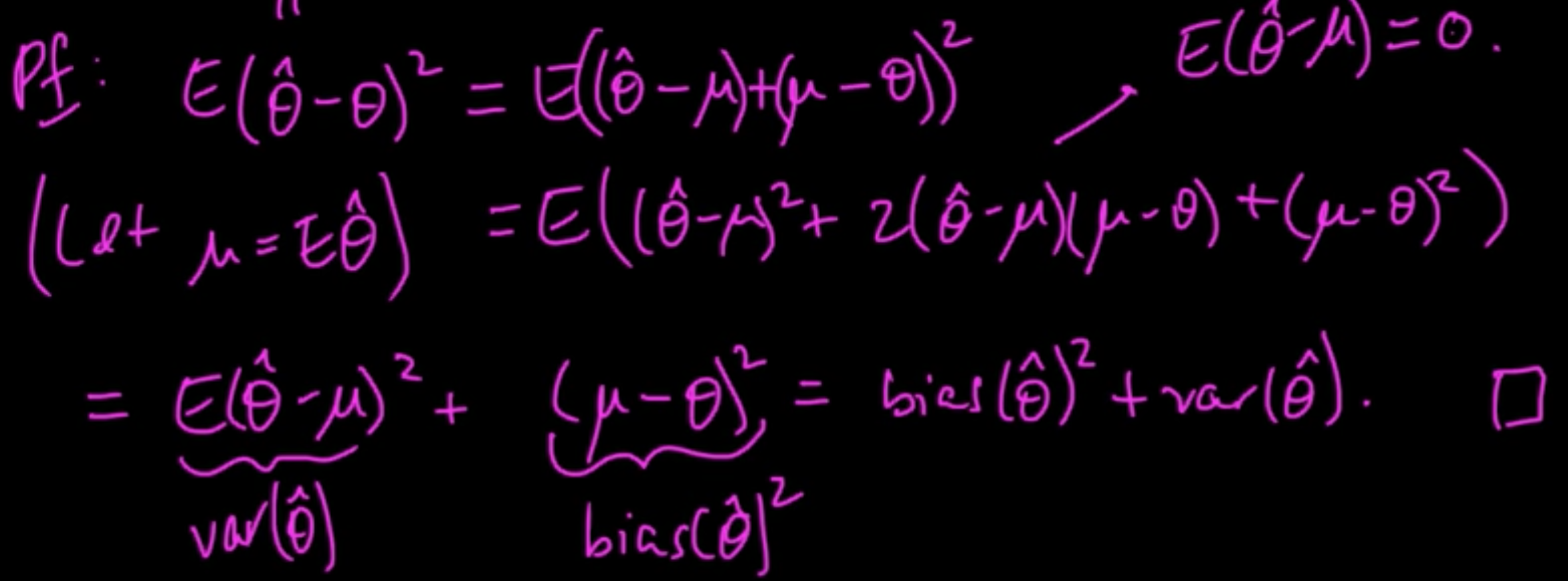
Silly example. $X \sim N(\theta, 1)$ where $\theta$ nonrandom & unknown and $D = X$
- “Natural” estimate of $\theta$ : $\delta_1(D) = X \leadsto$ bias$^2 = 0$, var$ = 1$, MSE$ =1$
- “Silly” estimate of $\theta$ : $\delta_0(D) = 0 \leadsto$ bias$^2 = \theta^2$, var$ = 0$, MSE$ = \theta^2$
cf. Shrinkage, Stein’s paradox
(ML 11.6) Inadmissibility
Recall. $R(\theta, \delta) = \mathbb{E}(L(\theta, \delta(D) \vert \theta)$.
Example. Target: $N(\theta, 1)$ where $\theta \in \mathbb{R}$.
Data: $D = (X_1, \ldots, X_n)$ where $X_i \sim (\theta, 1)$, iid.
Risk: $L(\theta, \delta) = (\theta - \delta)$.
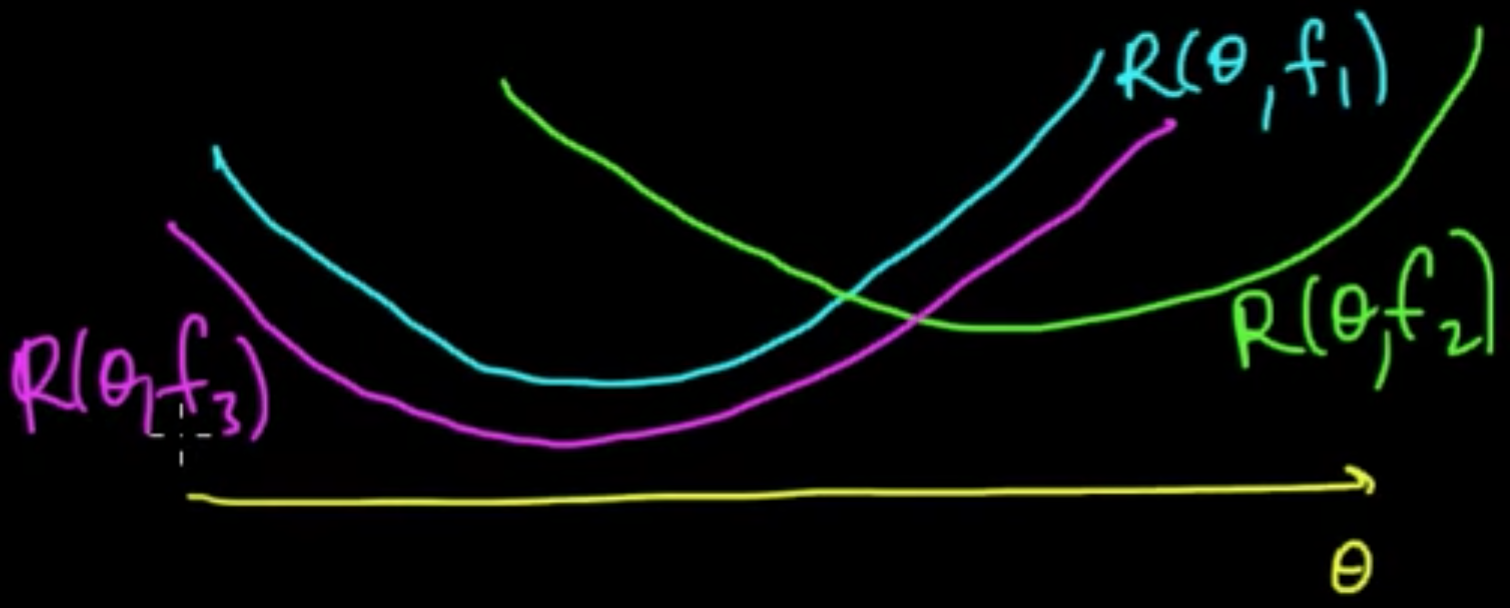
- “Natural” : $\delta^{(1)}_n(D) = X_n \leadsto$ $R(\theta, \delta^{(1)}) = 1$.
- “Silly” : $\delta^{(0)}_n(D) = 0 \leadsto$ $R(\theta, \delta^{(0)}) = \theta^2$.
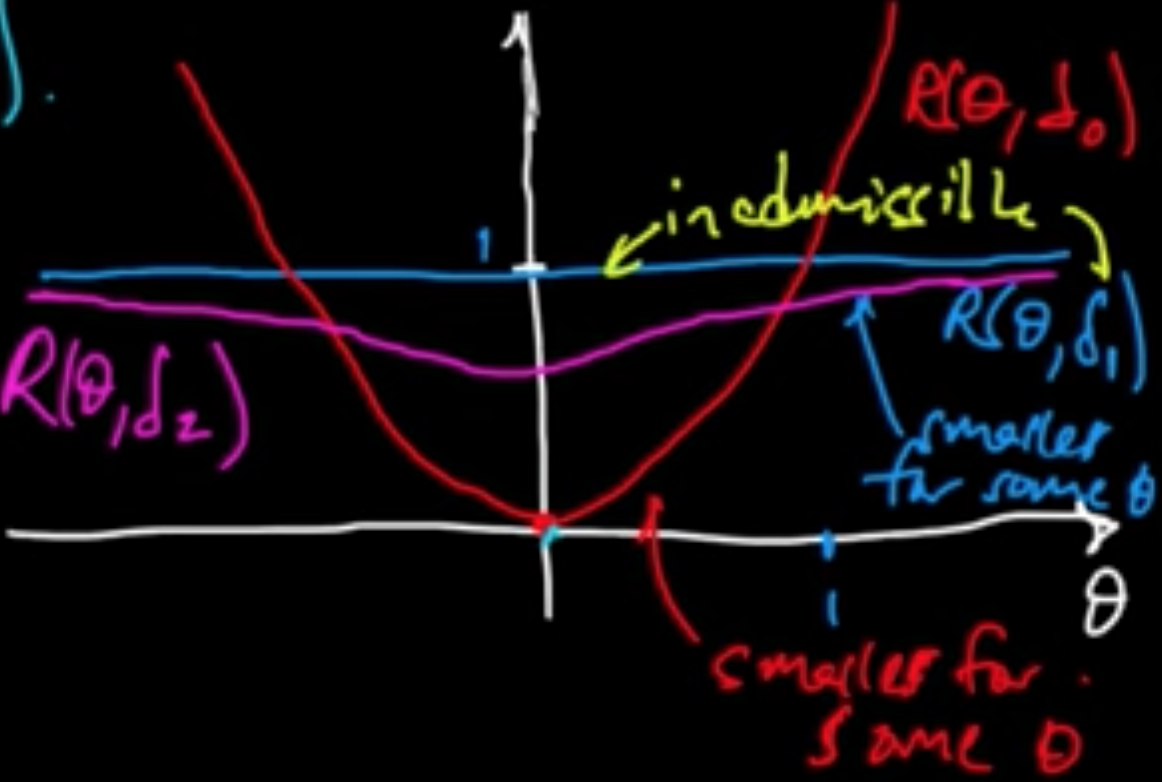
Definition. Given decision rules $\delta, \delta’$, we say $\delta$ dominates $\delta’$ if $R(\theta, \delta) \le R(\theta, \delta’)$ for all $\theta \in \Theta$ and $R(\theta, \delta) < R(\theta, \delta’)$ for some $\theta \in \Theta$.
Definition. A decision rule $\delta$ is inadmissible if there is another decision rule that dominates $\delta$. Otherwise, $\delta$ is admissible.
Fact. Both $\delta_1$ and $\delta_0$ are admissible.
(ML 11.7) A fun exercise on inadmissibility
Exercise. $X_1, \ldots, X_n \sim N(\mu, \sigma^2)$.
Assume $\mu$ is known.
Loss: $L(\sigma_1^2, \sigma_2^2) = (\sigma_1^2 - \sigma_2^2)^2$.
$\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n(X_i-\bar{x})^2$.
$s^2 = \frac{n}{n-1}\hat{\sigma}^2$
$s_c^2 = c\hat{\sigma}^2$, $c \ge 0$.
- Does $\hat{\sigma}^2$ dominates $s^2$? Or vice versa?
- Are $\hat{\sigma}^2$ and $s^2$ admissible?
- Is there a “best” $s_c^2$ for some $c \ge 0$?
(ML 11.8) Bayesian decision theory
Terminology.(Informal)
- A generalized Bayes rule is a decision rule $\delta$ that minimizes $\rho(\pi, \delta(D))$ for each $D$.
- A Bayes rule minimizes is a decision rule $\delta$ that minimizes $r(\pi, \delta)$.
Remark
- GBR $\Rightarrow$ BR, but BR $\not\Rightarrow$ GBR.
- If $r(\pi, \delta) = \infty$ for all $\delta$, then anything is a BR, but a GBR still makes sense.
- On a set of $\pi$-measure $0$, BR is arbitrary bit GBR is still sensible.
Complete Class Theorems. Under mild conditions:
- Every GBR (for a proper $\pi$) is admissible;
- Every admissible decision rule is a GBR for some (possibly improper) $\pi$
Check out the following :
- Complete Class Theorems for the Simplest Empirical Bayes Decision Problems
- A Complete Class Theorem for Statistical Problems with Finite Sample Spaces
Subscribe via RSS
