Notes on Machine Learning 5: MLE for Exponential Families

(ML 5.1) (ML 5.2) Exponential families

Definition. Let $\Theta \subset \mathbb{R}^k$. An exponential family is a set $\{p_\theta : \theta \in \Theta\}$ of MPFs or MDFs on $\mathbb{R}$ s.t.

$p_\theta = \exp\left( \sum_{i=1}^m \eta_i(\theta) s_i(\theta) \right) h(x)/z(x).$

$\theta \in \mathbb{R}^k$: parameter
$x \in \mathbb{R}^d$: “distritution variable”
$\eta_i : \Theta \rightarrow \mathbb{R}$
$s_i : \mathbb{R}^d \rightarrow \mathbb{R}$ (sufficient statistics)
$h : \mathbb{R}^d \rightarrow [0, \infty)$ (support & scaling)
$z : \Theta \rightarrow [0, \infty)$ (partition function: sort of normaizing constant but having very special properties)

$p_\theta(x) = e^{\eta(\theta)^Ts(x)}h(x)/z(\theta)$

($\eta = (\eta_1, \ldots, \eta_m)$, $s = (s_1, \ldots, s_m)$)

Example (Exponential distribution). (PDF)
Exponential($\theta$), $\theta \in \Theta = [0, \infty)$

$p_\theta(x) = \theta e^{-\theta x}I(x\ge 0)$

$\eta(\theta) = \theta$
$s(x) = -x$
$h(x) = I(x\ge 0)$
$z(\theta) = 1/\theta$
$k = d= 1$

Example (Bernoulli distribution). (PMF)
Bernoulli($\theta$), $\theta \in \Theta = (0, 1)$

$\begin{aligned} p_\theta &= \begin{cases} \theta, \, {\rm if} \,\,\, x=1 \\ 1-\theta, \, {\rm if} \,\,\, x=0 \\ 0, \, {\rm else} \end{cases} \\ &= \theta^{I(x=1)(1-\theta)^{I(x=0)}h(x)} \\ &= h(x)\exp \log \left( \theta^{I(x=1)}(1-\theta)^{I(x=0)}h(x) \right) \\ &= h(x)\exp \left( I(x=1)\log \theta + I(x=0)\log(1-\theta) \right) \\ \end{aligned}$

$\eta_1(\theta) = \log \theta$
$\eta_2(\theta) = \log (1-\theta)$
$s_1(x) = I(x=1)$
$s_2(x) = I(x=0)$
$h(x) = I_{\{0, 1\}}(x) = I(x \in \{0,1\})$

Not necessarily unique representation! :

$\begin{aligned} p_\theta &= \theta^{I(x=1)}(1-\theta)^{1-I(x=1)}h(x) \\ &= (1-\theta)\left(\frac{\theta}{1-\theta}\right)^{I(x=1)}h(x) \\ &= h(x)(1-\theta) \exp\left(I(x=1)\log \left(\frac{\theta}{1-\theta}\right) \right) \end{aligned}$

$\eta(\theta) = \log \left(\frac{\theta}{1-\theta}\right)$
s(x) = I(x=1)
$z(\theta) \frac{1}{1-\theta}$

Natural/Canonical form

$\eta(\theta) = \theta$ $\,$ ($m= k$)
$\eta_1(\theta) = \theta_1, \ldots, \eta_k(\theta) = \theta_k$

Example.

(PDF) Exponential, Normal, Beta, Gamma, Chi-square
(PMF) Bernoulli, Binomial, Poisson, Geometric, Multinomial

Properties of exponential families:

Conjugate prior
Maximum entropy

Example (NOT an exponential )family.

Uniform$(0, \theta)$

cf. Uniform$(0,a) = \frac{1}{a}I(x \in (0,a))$, for a fixed $a \in (0, \infty)$, gives an exponential family (trivially).

(ML 5.3) (ML 5.4) MLE for an exponential family

$p_\theta(x) = e^ h(x)/z(\theta)$

Given data $D = (x_1, \ldots, x_n)$ with $x_i \in \mathbb{R}^d$ gotten via $X_1, \ldots, X_n \sim p_\theta$ iid.

Wanna compute $\theta_{\rm MLE} = \arg\max_{\theta \in \Theta} p(D \vert \theta)$.

$\begin{aligned} p(D\vert \theta) &= \prod_{i=1}^n p(x_i \vert \theta) \\ &= \prod_{i=1}^n e^{\theta^T s(x_i)}h(x_i)/z(\theta) \\ &= z(\theta)^{-n} e^{\theta^T \sum_{i=1}^ns(x_i)} \\ &= z(\theta)^{-n} e^{\theta^T s(D)} \prod_{i=1}^n h(x_i) \end{aligned}$

$\log p(D \vert \theta) = -n\log z(\theta) + \theta^T s(D) + \sum_{i=1}^n \log h(x_i)$

$0 = \frac{\partial}{\partial \theta_j} \log p(D|vert\theta) = -n\frac{\partial}{\partial \theta_j} \log z(\theta) + s_j(D)$

where $\theta^Ts(D = \sum_{j=1}^k \theta_j s_j(D)$, $s_j(D) = \sum_{i=1}^n s_j(x_i)$ and $s=(s_i,\ldots, s_k)$.

Note $z(\theta) = \int_{\mathbb{R}^d} e^{\theta^T s(x)}h(x)dx$.

Then

$\begin{aligned} \frac{\partial}{\partial \theta_j} \log z(\theta) &= \frac{1}{z(\theta)} \frac{\partial}{\partial \theta_j} z(\theta) \\ &= \frac{1}{z(\theta)} \int s_j(x)e^{\theta^Ts(x)}h(x)dx \\ &= \int s_j(x) p_\theta(x)dx = E_\theta s_j(X) \end{aligned}$

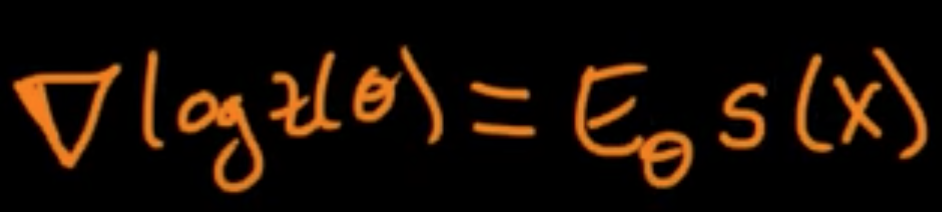
MLE for an exponential family

$\log p(D \vert \theta) = -n\log z(\theta) + \theta^T s(D) + \sum_{i=1}^n \log h(x_i) = -nE_\theta s_j(x) +s_j(D)$

implies

$n E_\theta s(X) = s(D) = \sum_{i=1}^n s(x_i)$

implies

$E_{\theta_{\rm MLE}} s(x) = \frac{1}{n}\sum_{i=1}^n s(x_i)$ if MLE exists and $\theta_{\rm MLE} \in {\rm Int} \Theta$.

Example. $p_\theta(x) = \theta e^{-\theta x} I(x \ge 0)$
$z(\theta) = \frac{1}{\theta}$, $s(x) = - x$, $\eta(\theta) = \theta$.

$\begin{aligned} \frac{\partial}{\partial \theta} \log z(\theta) &= \frac{\partial}{\partial \theta} -\log \theta \\ &= -\frac{1}{\theta} = E (s(X)) = -E(X) \end{aligned}$

implies $E(X \frac{1}{\theta})$.

Now $-\frac{1}{\theta} = E_\theta s(X) = \frac{1}{n}\sum_{i=1}^n (-x_i)$ implies
$\frac{1}{\theta} = \frac{1}{n}\sum_{i=1}^n x_i$ implies

$\theta_{\rm MLE} =\frac{1}{\frac{1}{n}\sum_{i=1}^nx_i}$