Notes on Probability Primer 2: Conditional probability & independence

(PP 2.1) Conditional Probability

Conditinoal probability and independence are critical topics in applications of probability.

Notation “Suppress” $(\Omega, \mathcal{A})$. Whenever write $P(E)$, we are implicitly assuming some underlying probability measure sapce ($\Omega$, $\mathscr{A}$ $p$).

Terminology

event = measureable set = set in $\mathcal{A}$
sample space = $\Omega$

Definition Assuming $P(B) > 0 $, define the conditional probability of $A$ given $B$ as

$P(A \vert B) = \frac{P(A \cap B)}{P(B)}.$

(PP 2.2) Independence

Definition. Eventa $A< B$ are independent if $P(A \cap B) = P(A)P(B)$.

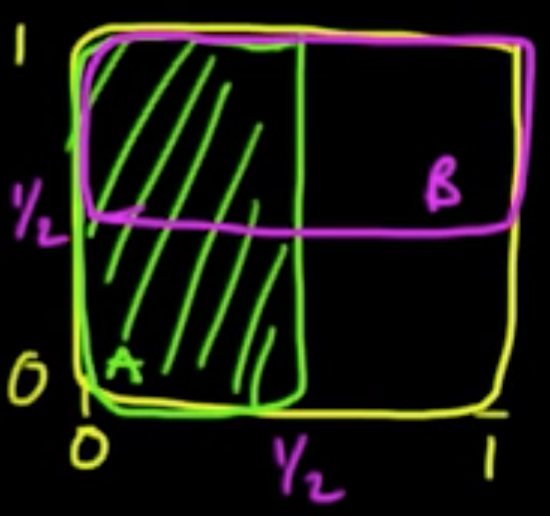
Independence

Definition. Eventa $A_1, \ldots, A_n$ are (mutually) independent if for any $S \subset \{1, \ldots, n\}$,

$P(\cap_{i \in S} A_i) = \prod_{i \in S} P(A_i).$

Remark. Mutual independence $\Rightarrow$ pairwise independence

Warning! Pairwise independence $\nRightarrow$ mutual independence

Pairwise independence $\nRightarrow$ mutual independence

Definition. $A, B$ are conditionally independent given $C$ (where $P(C) >0$) if

$P(A\cap B \vert C) = P(A \vert C)P(B \vert C).$

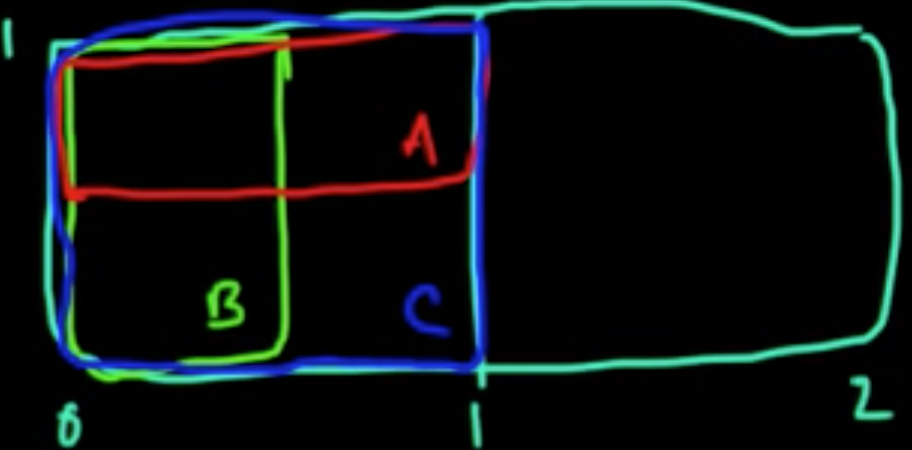
Conditional independence

Remark. Independence $\nRightarrow$ conditional independence

(PP 2.3) Independence (continued)

Definition. Eventa $A_1, A_n, \ldots$ are (mutually) independent if for any finite $S \subset \{1, \ldots, n\}$,

$P(\cap_{i \in S} A_i) = \prod_{i \in S} P(A_i).$

Definition. $A_1, \ldots, A_n$ are conditionally independent given $C$ (where $P(C) >0$) if

$P(\cap_{i \in S} A_i\vert C) = \prod_{i \in S} P(A_i\vert C).$

Proposition. Suppose $P(B)>0$. Then $A, B$ are independent iff $P(A\vert B) = P(A)$.

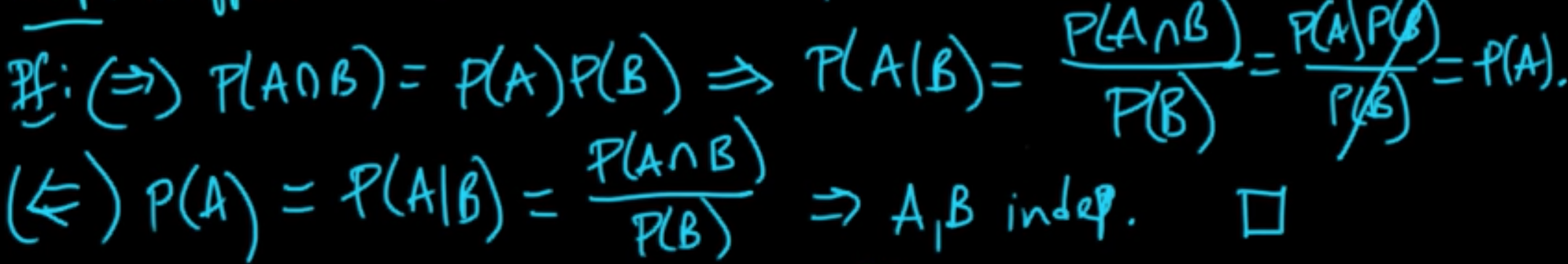
Exercise.

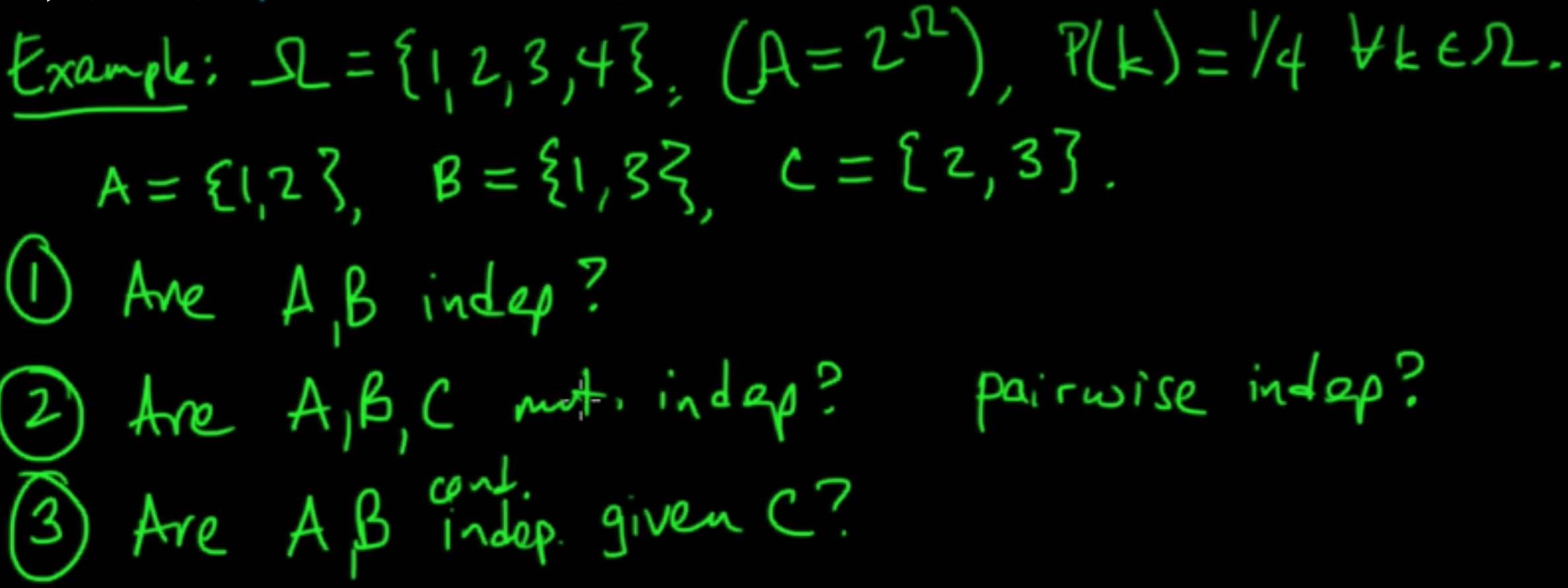
(PP 2.4) Bayes’ rule and the Chain rule

3 rules: Bayes’, Chain, Partition

Remark. $P(A \cap B) = P(A \vert B)P(B)$ $\,$ if $P(B) >0$. (In fact, the equality holds even when $P(B) = 0$!)

Theorem (Bayes’ rule)

$P(B \vert A) = \frac{P(A\vert B)P(B)}{P(A)}$

if $P(A), P(B) >0$.

Plays an important role in particular in Bayesian statistics.

Theorem (Chain rule) If $A_1, \ldots, A_n$ satisfy $P(A_1 \cap \cdots \cap A_n) >0$, then

$P(A_1 \cap \cdots \cap A_n) = P(A_1)P(A_2 \vert A_1)P(A_3\vert A_1\cap A_2)\cdots P(A_n\vert A_1 \cap \cdots \cap A_{n-1}).$

Proof. By induction.

(PP 2.5) Partition rule, conditional measure

Definition A partition of $\Omega$ is a nonempty (finite or countable) collection $\{B_i\} \subset 2^\Omega$ s.t.

$\cup_i B_i = \Omega$
$B_i \cap B_j = \emptyset$ if $i \neq j$

Theorem (Partition rule) $P(A) = \sum_i P(A \cap B_i)$ for any partition $\{B_i\}$ of $\Omega$

Proof: $A = A \cap \Omega = A \cap (\cup_i B_i) = \cup_i (A \cap B_i)$
$P(A) = P(\cup_i (A\cap B_i)) = \sum_i P(A \cap B_i)$

Definition. If $P(B) >0$, then $Q(A) = P(A \vert B)$ defines a probability measure $Q$ (conditional probability measure given $B$).

Exercise.

Bayes’ rule for cond. prob. meas.:
Chain rule for cond. prob. meas.:
Partition rule for cond. prob. meas.: