Notes on Convex Optimization

In this page I summarize in a succinct and straighforward fashion what I learn from Convex Optimization course by Stephen Boyd, along with my own thoughts and related resources. I will update this page frequently, like every week, until it’s complete.

Acronyms

LA: Linear Algebra

Preceding materials to be added..

(Lecture 9) Numerical linear algebra background

The main goal of the third and the last section (Lectures 9–12) of the course is to demystify how it is that we solve these convex optimization problems.

It is very important for everyone to know a little bit about how these problems are solved, and specifically the link between problem structure and how fast we can solve it.

Matrix structure and algorithm complexity

Cost of solving linear system $Ax = b$ ($A \in \mathbb{R}^{n\times n})$ :

$n^3$, for general methods
less, if $A$ is structured (banded, sparse, Toeplitz, etc)

FLOP counts

Linear equations that are easy to solve

Diagonal : $n$ flops
Lower triangular : $n^2$ flops via forward substitution
Upper triangular : $n^2$ flops via backward substitution
Orthogonal : $2n^n$ flops
Permutation : $0$ flops

The factor-solve method for solving $Ax = b$

Factor
Solve

“Factorization dominates everything!”

$LU$ facorization (completely equivalent to Gaussian elimination)

Cholesky factorization

$LDL^{\rm T}$ factorization

Equations with structured sub-blocks

Structured matrix plus low rank term

(Lecture 10) Unconstrained minimization

Descent methods

Gradient descent

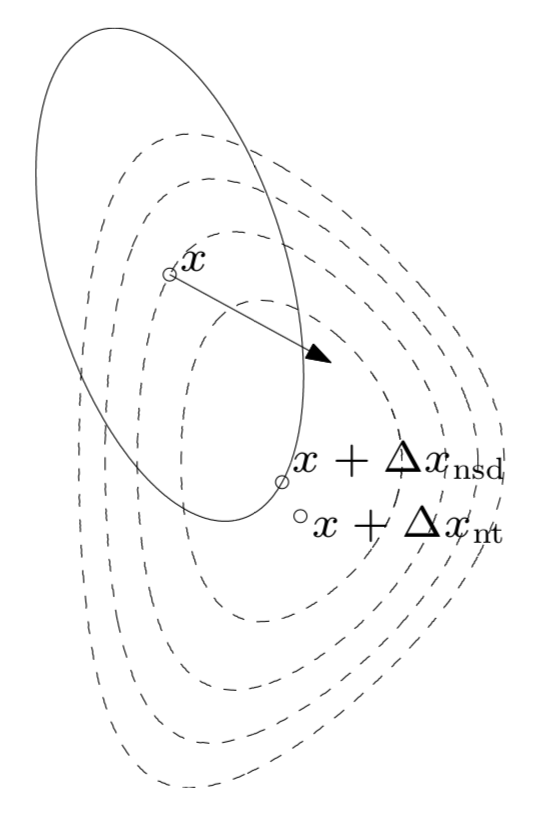
Steepest descent method

Newton’s method

Newton’s method by G. Strang
(ML 15.1) Newton’s method (for optimization) - intuition
(ML 15.2) Newton’s method (for optimization) in multiple dimensions

Newton step: $\Delta x_{\rm nt} = - \nabla f(x)^{-1}\nabla f(x)$

$x + \Delta x_{\rm nt}$ minimizes 2nd order approximation (by a quadratic model):

$\hat{f}(x + v) = f(x) + \nabla f(x)^T v +\frac{1}{2}v^T \nabla^2f(x)v$

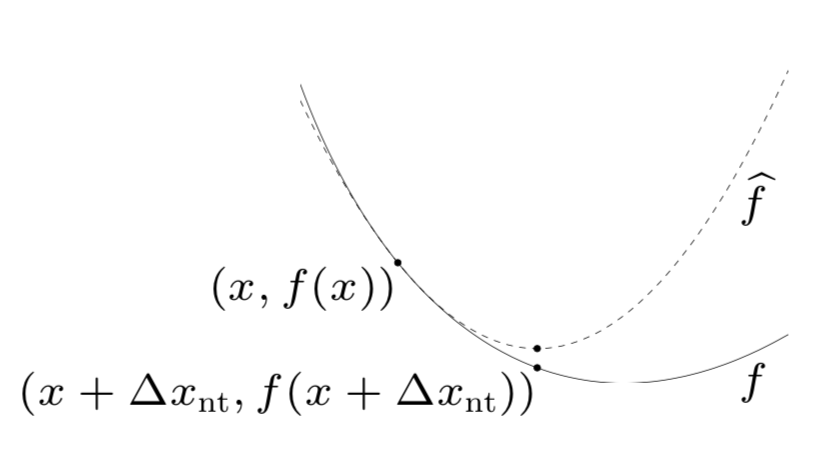
$x + \Delta x_{\rm nt}$ solves linearized optimality condition:

$\nabla f(x + v) \approx \nabla\hat{f}(x = v) = \nabla f(x) + \nabla^2 f(x)v = 0$

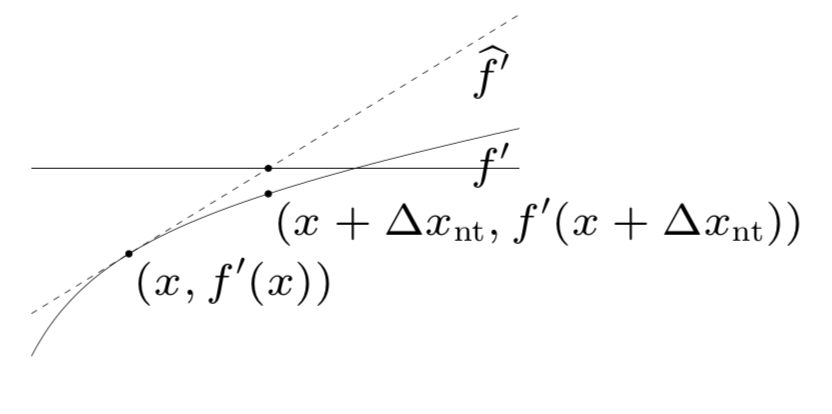
$x + \Delta x_{\rm nt}$ is steeptest ditection at $x$ in local Hessian norm:

$\Vert u \Vert_{\nabla^2f(x)} = (u^T \nabla^2 f(x)u)^{\frac{1}{2}}$

Dashed lines are contour lines of $f$, the ellipse is \\{x+v : v^T \nabla^2 f(x)v=1\\}, and the arrow shows the direction of $-\nabla f(x)$.

Newton decrement: a measure of the proximity of $x$ to $x^*$

$\lambda(x) = (\nabla f(x)^T \nabla^2 f(x)^{-1} \nabla f(x))^{\frac{1}{2}}$

very good estimate, if you’re close, of $f(x) - p^*$ using quaratic approximation $\hat{f}$:

$f(x) -\inf_y \hat{f}(y) =\frac{1}{2}\lambda(x)^2$

(provides way better stopping criteria than gradient!)

equal to the norm of the Newton step in the quadratic Hessian form:

$\lambda(x) = (\Delta x_{\rm nt}^T \nabla^2 f(x) \Delta x_{\rm nt})^{\frac{1}{2}}$

directional derivative in the direction:

$\nabla f(x)^T \Delta x_{\rm nt} = - \lambda(x)^2$

affine invariant! (unlike the gradient $\Vert \nabla f(x) \Vert_2$)

Algorithm (Newton’s method)
given a starting point $x \in {\rm dom} (f)$ and tolerance $\epsilon >0$
repeat
$ \,\,\,\,\,\,\,\,$ 1. compute the Newton step and decrement:
$ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ $\Delta x_{\rm nt} = - \nabla f(x)^{-1}\nabla f(x)$
$ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ $\lambda(x) = (\nabla f(x)^T \nabla^2 f(x)^{-1} \nabla f(x))^{\frac{1}{2}}$
$ \,\,\,\,\,\,\,\,$ 2. stopping criterion: quit if $\lambda^2/2 \le \epsilon$
$ \,\,\,\,\,\,\,\,$ 3. line search: choose step size $t$ by backtracking line search
$ \,\,\,\,\,\,\,\,$ 4. update: $x \leftarrow x + t\Delta x_{\rm nt}$

To be added..