(ML 1.1) What is machine learning?

“Designing algorithms for inferring what is unknown from knowns.”

MM considers ML as a subfield of statistics, with emphasis on algorithms.

Got to read an interesting article Machine Learning vs. Statistics, thanks to Whi Kwon.

Applications

  • Spam (filtering out)
  • Handwriting (recognition)
  • Google streetview
  • Netflix (recommendation systems)
  • Navigation
  • Climate modelling

(ML 1.2) What is supervised learning?

Classification of ML problems: Supervised vs. Unsupervised

Supervised: Given $(x^{(1)}, y^{(1)}), \ldots, (x^{(n)}, y^{(n)})$ choose a function $f(x) = y$.

  • Classification: $y^{(i)} \in \{$finite set$\}$
  • Regression: $y^{(i)} \in \mathbb{R}$ or $y^{(i)} \in \mathbb{R}^d$
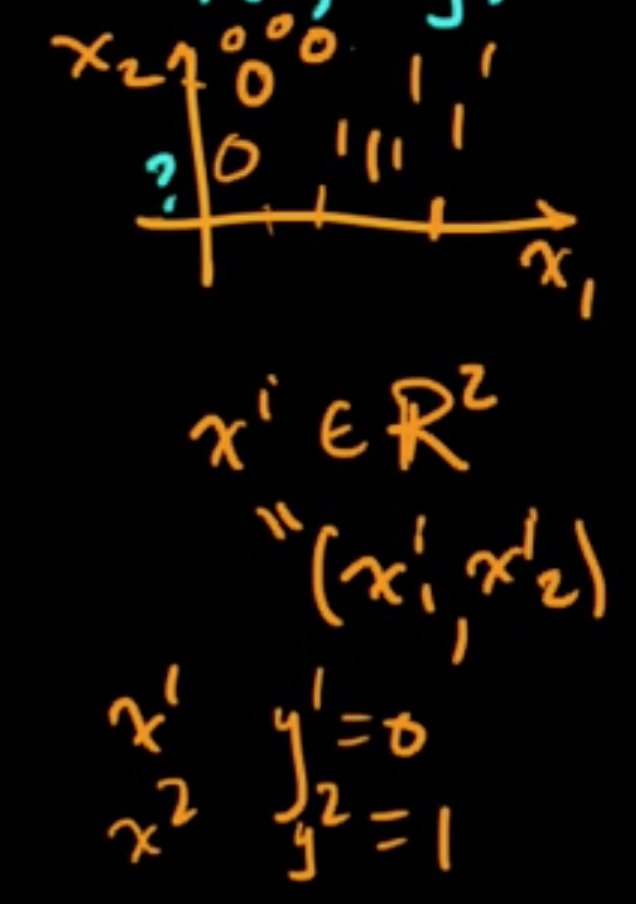
Classification
Classification
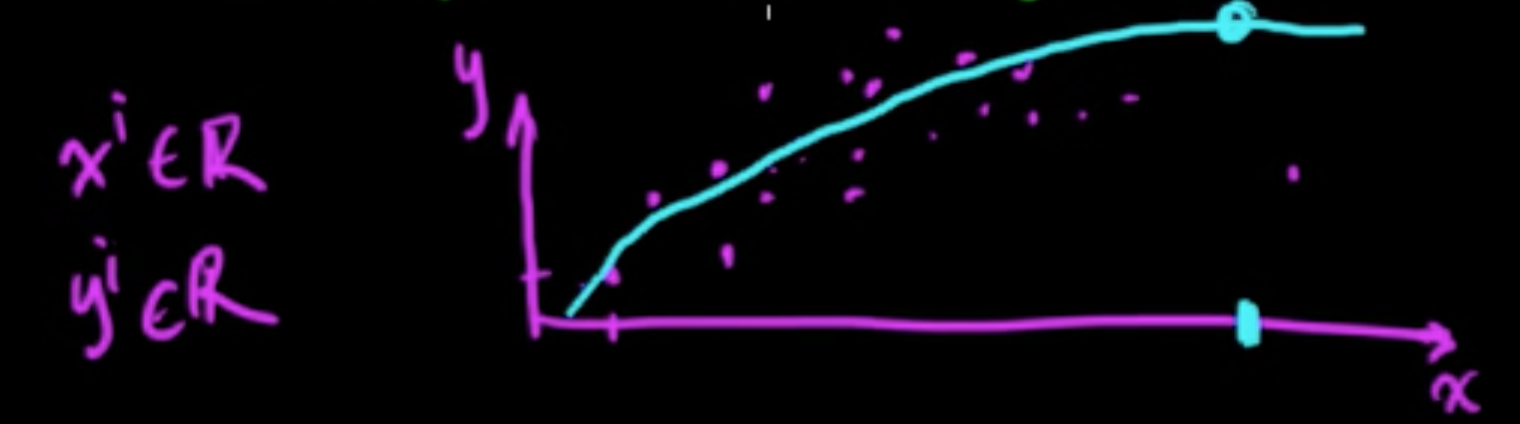
Regression
Regression
  • $x^{(i)}$ : data point
  • $y^{(i)}$ : class/value/label

(ML 1.3) What is unsupervised learning?

Much less well-defined.

Unsupervised: Given $x^{(1)}, \ldots, x^{(n)}$, find patterns in the data.

  • Clustering (typical UL)
  • Density estimation (much more well-defined)
  • Dimensionality reduction
  • Feature leraning
  • many more
Clustering
Clustering
Density estimation and Dimensinality reduction
Density estimation and Dimensinality reduction

(ML 1.4) Variations on supervised and unsupervised

  • Semi-supervised
  • Active Learning
  • Decision theory
  • Reinforcement Learning

(ML 1.5) Generative vs discriminative models

Given data $(x^{(1)}, y^{(1)}), \ldots, (x^{(1)}, y^{(1)})$.
Denote $(x, y)$ by a prototypical (data point, label) pair.

Discriminative: model $p(y\vert x)$

Generative: model the joint distribution

Some good reasons to use discriminative model: Statistically, it’s very hard to estimate either $f(x\vert y)$ or $f(x)$ because it take a lotof data. (You’re inclined to make mistakes.)

Generative process:

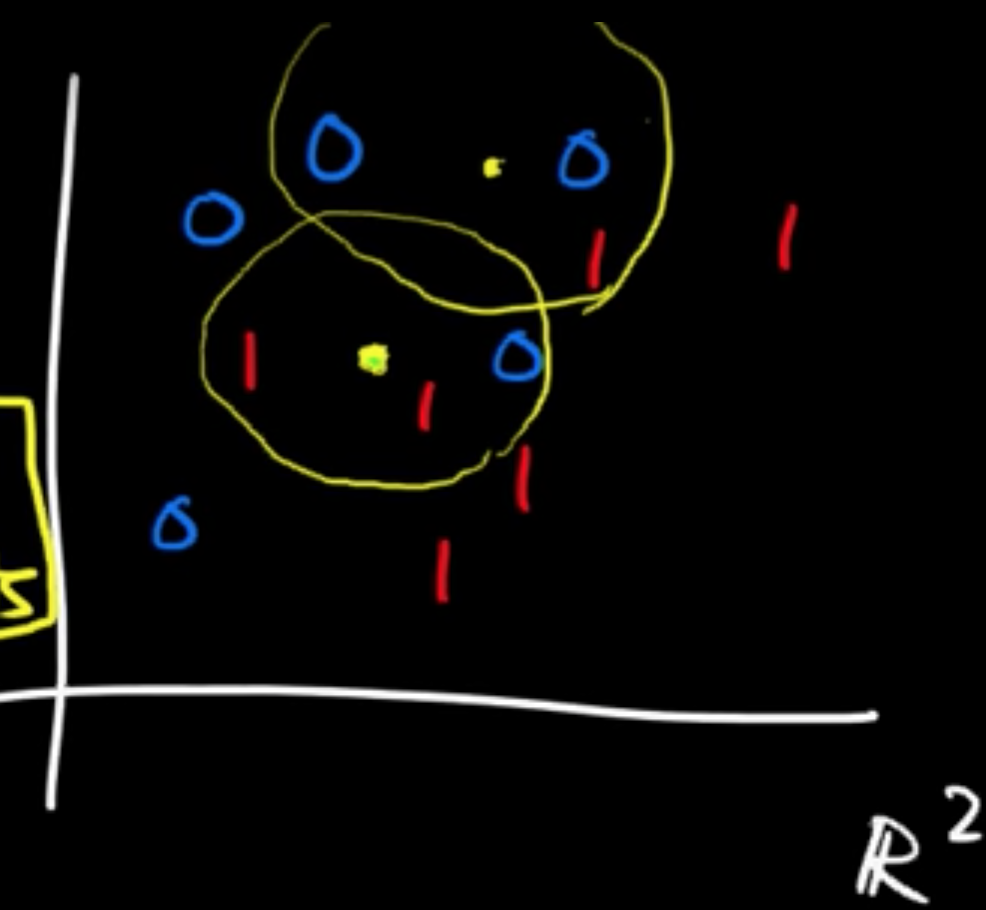
(ML 1.6) $k$-Nearest Neighbor (kNN) classification algorithm

Given data $D = ((x_1, y_1), \ldots, (x_n, y_n))$, $x_i \in \mathbb{R}, y_i \in \{0, 1\}$.
Given a new data point $x$.

Classify by deciding on what is $y$ corresponding to $x$ according to the majority vote from the $k$-nearest points in the training data.

(Nearest in terms of a pre-determined metric.)

3NN
3NN in Euclidean metric

Probabilistic formulation (Discrimitive model!) Fix $D$, $x$, $k$.

Find a random variable $Y \sim p$ where $p(y) =$ #$\{x_i \in N_k(x) : y_i = y \}/k$

Sometimes people write $p(y\vert x, D)$ for $p(y)$, even though it’s not really a conditional probability.

The estimate (or prediction) is given by

How does one choose $k$?
$\leadsto$
Important problem of choosing parameters. (Cross-validation / Bias-variance trade-off)