일차함수와 직선의 방정식

시리즈: 고등학교 수학으로 이해하는 선형대수

1. 일차함수와 직선의 방정식
2. 두 직선의 관계
3. 평면 위에서의 선형대수

함수와 방정식

수학에서 두 가지 양, 혹은 그 양을 표현하는 두 변수, 사이의 관계를 기술하는 방법론 두 가지가 있다. 방정식과 함수가 그것이다. 자연스럽게 세 변수 이상의 경우로 확장할 수 있지만 두 변수 경우만으로도 본질적인 아이디어를 이해하는데 충분하다.

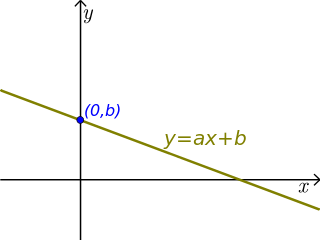
일차방정식과 일차함수의 경우를 들어 이해해보자. 일차함수는 보통 다음 식으로 표현된다.

이 식이 일차함수의 표현이 되기 위해서는 기울기라고 불리는 수 $a$가 $0$이 아닌 실수이어야 하는데, 그래야만 우변의 식 $ax+b$가 일차식이 되기 때문이다. 기울기 $a=0$인 경우 함수 $y=b$는 일차함수가 아닌 상수함수가 된다.

평면 위의 직선의 방정식

평면 위의 직선 중에 일차함수와 상수함수로 기술되지 않는 나머지 모든 경우는 $x=c$ 형태의 일차방정식으로 표현된다. 요약하면,

1. 수직선은 $x=c$ 형태의 일차방정식으로,
2. 수평선은 $y=b$ 형태의 일차방정식으로,
3. 나머지 직선들은 $y=ax+b$ 형태의 방정식으로

표현된다. 특히 2, 3번의 방정식은 $x$를 독립변수, $y$를 종속변수로 하는 함수의 성질을 가지게 되고 각각 상수함수와 일차함수가 된다.

이 세 가지 모든 경우를 일괄적으로 나타내는 방법은 다음의 일차방정식을 이용하는 것이다.

방정식으로 두 변수의 관계를 표현하는 것이 상대적으로 좀 더 일반적인 방법이어서 더 다양한 관계들을 표현할 수 있는 반면, 함수의 개념은 방향성(혹은 기능성)이 있는 관계를 좀 더 정밀하게 기술하는 장점이 있다. 여기에 대해서는 추후에 좀 더 자세히 알아보기로 하자.

대수와 기하

수학에서 다항식으로 표현된 방정식과 그 해를 연구하는 분야를 대수 혹은 대수학이라고 부른다. 영어로는 algebra라고 표현하는데 흥미롭게도 이 영단어는 알고리즘(algorithm)과 같은 어원을 가진다.

공간과 도형을 연구하는 수학 분야를 기하 또는 기하학이라고 부르는 것은 익히 알고있을 것이다. 평면 위의 직선이라는 기하학적 물체를 방정식을 통해 공부할 수 있다는 사실은 당연한 것 처럼 보이지만 사실 이런 방법론은 17세기에 와서야 데카르트와 페르마에 의해 독립적으로 발명되었다. 좌표계를 도입하여 수와 방정식을 통해 기하를 대수적으로 공부하는 이 방식은 해석기하학 혹은 좌표기하학, 카티션기하학 등의 이름으로 불리운다.

일차함수

일차함수 $y=ax+b$의 경우를 조금 자세히 분석해보면, 일차함수는 기울기 $a$와 $y$ 절편 $b$, 두 수(파라미터라고도 불리운다)에 의해 완전히 기술된다. 기울기가 $a$라는 의미를 그래프의 관점에서 살펴보면, 일차함수의 그래프는 (투자 관련 차트를 기술하는 용어를 빌어 표현하자면) $a$가 양수인 경우 우상향, $a$가 음수인 경우 우하향 직선이다.

요약:

평면 위의 모든 직선은 다음 형태의 일차방정식으로 기술된다:

일차방정식이기 위해 $a\neq0$이거나 $b\neq0$이다.

1. 수직선은 $x=c$
2. 수평선은 $y=b$ (상수함수)
3. 나머지 직선은 $y=ax+b$ (기울기 $a\neq 0$, 일차함수)

덧붙이는 말:

@Hyunggi Chang 님, 피드백 감사합니다.