Incremental means and updates

시간의 이산적인 흐름에 따라 새로운 데이터들이 수집될 때 매번 그 평균을 구해야 하는 상황이 종종 발생한다. 새로운 데이터가 들어올 때마다 평균을 정의에 의해 계산하는 것은 매우 비효율적이다. 반면 이전 스텝까지 계산된 평균을 이용하여 상대적으로 빠르게 계산할 수 있는 방법이 있다.

시간이 $t=1, 2, \ldots$ 와 같이 변함에 따라 수집되는 데이터를 $x_1 ,x_2, \ldots$ 순으로 나타내자. 이때 시점 $t= 1$부터 $t = n$까지의 데이터의 평균을 $\mu_n$이라고 하자. 평균의 정의에 의하면

만일 시점 $t = n-1$까지의 평균 $\mu_{n-1}$을 이미 알고 있다면 (혹은 계산을 했다면), $\mu_n$을 다음 식으로 구할 수 있다.

즉, 직전까지의 평균 $\mu_{n-1}$과 새로운 데이터 $x_n$ 만을 이용하여 현시점의 평균 $\mu_n$를 구할 수 있다. 이 식은 다음과 같이 간단하게 증명된다.

자 이제 이 유용한 식의 의미를 식 자체로부터 읽어내 보려고 한다.

사실 본질에서는 위의 증명을 풀어쓴 효과와 같다고 할 수 있지만 그림을 이용하여 좀 더 직관적으로 머릿속에 정리해보는 데 의의가 있을 것 같다.

$t = 1$부터 $t = n-1$까지의 데이터가 다음과 같이 주어졌다고 하자. (그림에서는 $n = 5$이다.)

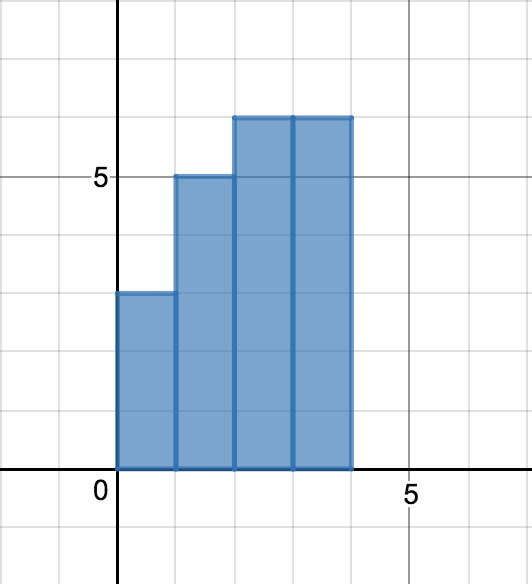
시점 $t-1$까지의 평균이 $\mu_{t-1}$이므로 평균의 관점에서만 보면 $\mu_{t-1}$인 데이터가 $t-1$개 있는 것과 다름없다.

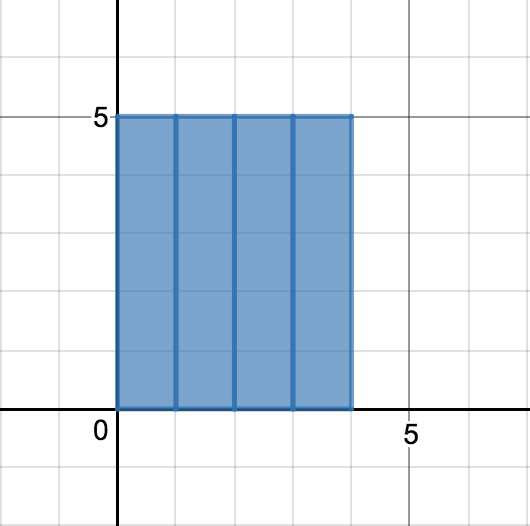
이제 $n$번째 (새로운) 데이터 $x_n$이 주어진다.

먼저, 새롭게 수집된 데이터 $x_n$이 이전 평균 $\mu_{n-1}$과 같은 경우를 생각해보자.

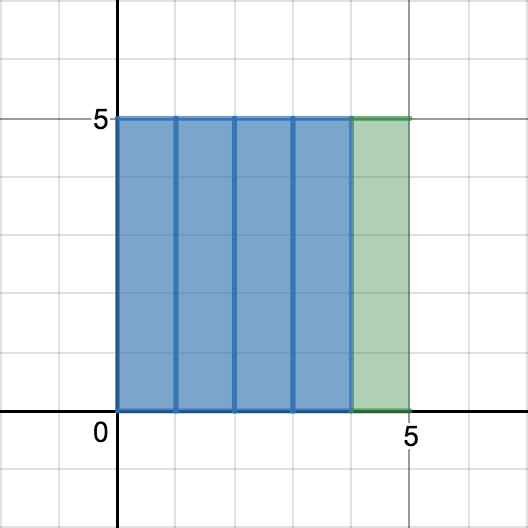
평균 $\mu_n$은 얼마인가? 그렇다. 바로

기존의 평균과 같은 데이터가 수집되면 평균은 그대로 유지됨을 쉽게 알 수 있다.

이번엔 평균보다 큰 데이터가 새로 수집된 상황을 생각해보자.

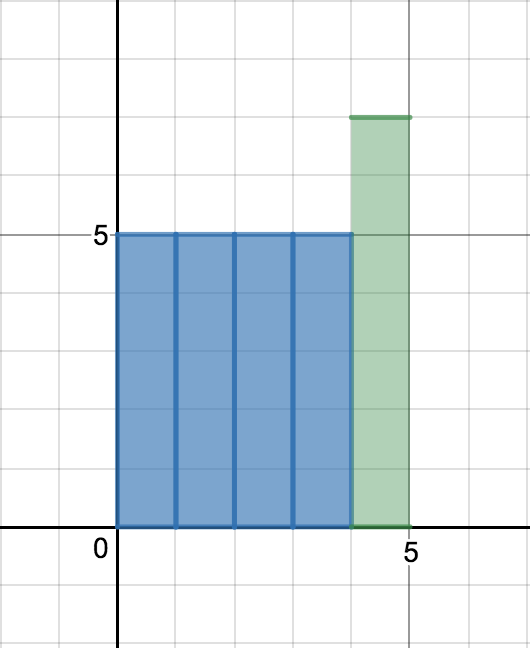
이제 $\mu_n$은 더 이상 $\mu_{n-1}$과 같지 않고 어떤 양을 조금 더해주어야만 할 것 같다. 즉, 기존의 평균과 차이나는 만큼을 반영하여 업데이트 시켜주어야 한다. 어떻게 하면 이 작업을 손쉽게 할 수 있을까?

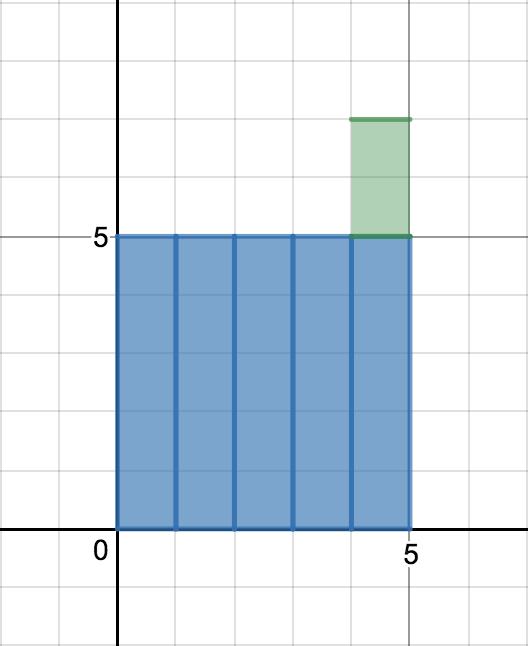
잠시 생각을 해보자..

아마 어렵지 않게 다음과 같은 생각을 하게되지 않을까?

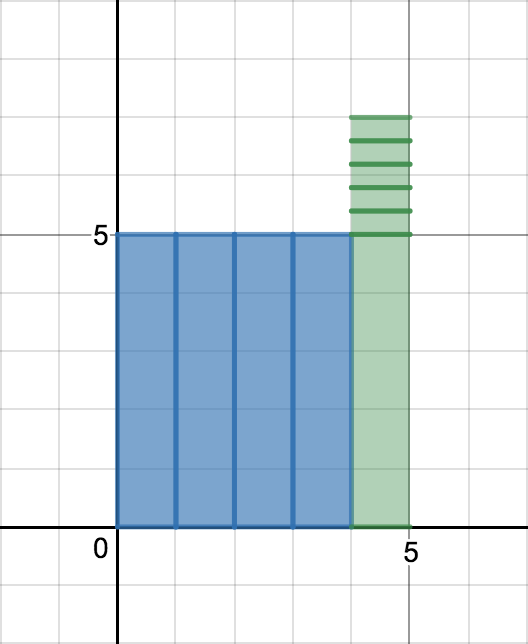
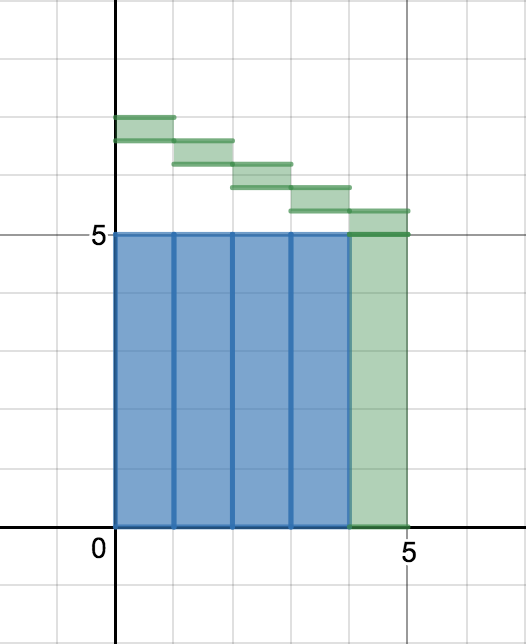
그림 6과 같이 새 데이터 $x_n$에서 기존의 평균 $\mu_{n-1}$을 초과하는 양 $x_n - \mu_{n-1}$을 $n$개로 쪼갠다. 그리고 이렇게 생긴 크기 $\frac{1}{n}(x_n - \mu_{n-1})$인 $n$ 조각을 각 시점의 데이터에 분배한다. (그림 7, 8, 9)

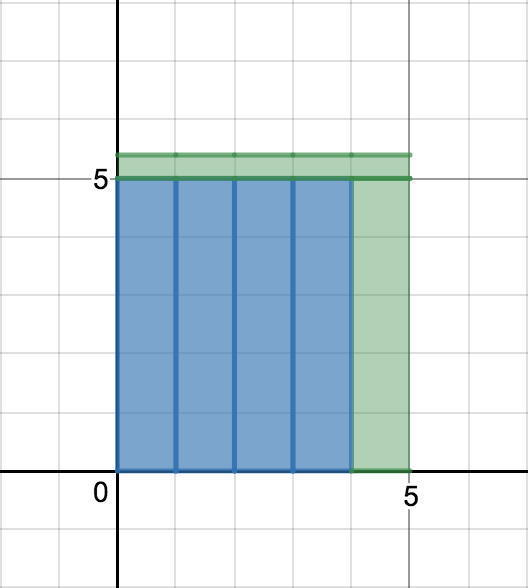
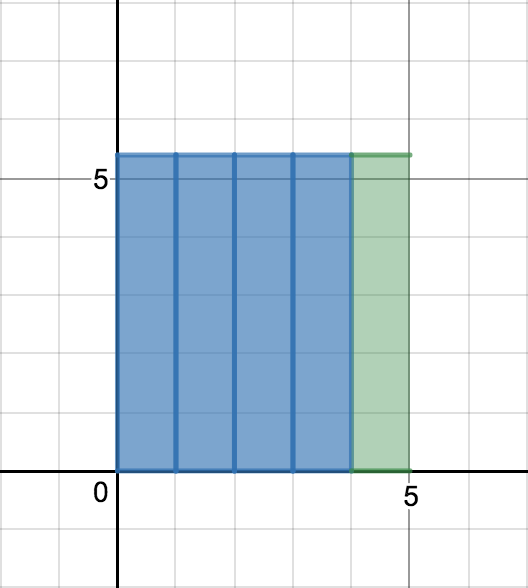
이제 현 시점의 평균이

을 만족함을 쉽게 알 수 있다.

마지막으로, 새로운 데이터 $x_n$이 $\mu_{n-1}$보다 작은 경우는 어떻게 해야 할까? 새 데이터와 이전 평균의 차 $x_n - \mu_{n-1}$이 음수가 된다. 이 경우를 직접 확인해보는 것이 이제까지의 내용을 정리해보는 매우 좋은 방법인 듯 하다. 자세한 내용은 여러분들께 맡긴다.

Constant step-size parameter

강화학습 알고리즘을 디자인할 때 많은 경우 시작 시점부터 현시점까지의 스텝 수 $n$을 항상 기록해가면서 평균을 계산해나가기에 불편한 면이 있고 (특히 상당히 큰 $n$을 다뤄야 하는 경우), 이런 경우 오래된 과거 시점의 데이터들에 대한 세밀한 정보를 어느 정도 잊어버리고 현재 가지고 있는 대푯값(예를 들어 평균)을 새롭게 수집된 데이터와 비교하여 그 차이에 대한 정보를 빠르게 업데이트해주는 것이 필요하다. 따라서 실제 평균을 정확히 구해서 유지해나가기보다는 평균을 구하는 식

을 조금 변형하여 새로운 “대푯값”을 업데이트해가는 방법을 이용하게 된다.

여기서 $\alpha$는 step-size parameter라고 불리는 상수로 시간 $t$에 무관하며, 수렴의 문제를 고려하여 $0<\alpha<1$인 값을 선택하게 된다. 또한, 많은 경우 새로운 데이터 $x_n$을 그대로 이용하지 않고 상황에 따라 적절히 변형한 $\tilde{x}_n$을 이용하여 업데이트하게 된다.

변수 $\mu, \tilde{x}$를 이용한 pseudocode에서는 보통 다음과 같은 형태로 표시된다.

참고자료

[1] R. Sutton, A. Barto, Reinforcement leaning: an introduction, second edition (final draft).
[2] D. Silver, RL Course, Lecture 4: Model-free Prediction.

읽으시다 오류나 부정확한 내용을 발견하시면 꼭 알려주시길 부탁드립니다. 감사합니다.