확률변수를 이해하다

불확실성이 포함된 상황을 체계적으로 기술하기 위해 수학의 확률이란 개념을 이용하게 된다. 작년 이맘때쯤 확률의 개념이 어떻게 탄생하게 되었는지 그 역사적 배경에 관한 김민형 교수님의 공개강연이 있었다. 고맙게도 온라인상에 동영상이 올라와 있으니 시청을 권한다 [2]. 강연의 내용 중 인상 깊었던 것 하나는 확률 개념이 탄생하던 17세기 유럽 그 시대의 석학들에게도 난제였던 문제를 이 시대 우리들은 고등학생들도 그리 어렵지 않게 해결하는 수준이 되었다는 사실이다. 그래서 우리는 자부심을 좀 가져도 된다는.

확률 개념을 본격적으로 살펴보기 전에 먼저 고려해야 하는 것이 이산과 연속의 구분이다. 측도론(measure theory)이라는 수학 이론을 이용하면 이산(discrete)과 연속(continuous)의 확률 개념을 통합적으로 다루는 것이 가능하지만, 이 포스트에서는 이산의 경우만을 다루기로 한다. 측도론을 이용한 통합적인 접근법을 이해하기 위해서는 Mathematical Monk의 동영상 강의를 강력히 추천한다 [3]. 측도론을 통하여 확률론이 현대적인 엄밀한 학문으로 확립된 것은 Kolmogorov 라는 러시아 수학자의 업적으로 알려져 있다.

확률함수(probability, probability function)

확률에 관련된 논의는 확률이라는 함수로부터 시작하는 것이 좋을 것 같다. “확률”이란 단어는 특정한 성질을 만족하는 함수라는 수학적 개념은 물론 더욱 일반적인 의미로도 사용되기 때문에 이 글에서는 확률함수라는 이름으로 수학적 확률 개념을 지칭하기로 한다. 확률함수(probability function)는 특정 조건을 만족하는 $p: {\mathscr P}(\Omega) \rightarrow [0,1]$ 형태의 함수이다. 여기서 $\Omega$를 표본공간(sample space), 표본공간의 원소를 표본(sample)이라 부른다. 표본공간 $\Omega$의 모든 부분집합을 원소로 하는 집합을 ${\mathscr P}(\Omega)$로 나타낸다. 즉, ${\mathscr P}(\Omega)$의 원소 $A$는 $\Omega$의 부분집합이다:

$A \subset \Omega \Leftrightarrow A \in {\mathscr P}(\Omega).$

이런 $A$를 사건(event)이라고 한다.

확률함수의 특정 조건이란 다름 아닌 다음 세 가지 성질이다.

모든 $A \in {\mathscr P}(\Omega)$에 대해서 $0 \le p(A) \le 1$;
$p(\Omega) = 1$;
$A, B \in {\mathscr P}(\Omega)$가 교집합이 없으면, $p(A \cup B) = p(A) + p(B)$. (덧셈 원리)

표본공간 $\Omega = \{⚀, ⚁, ⚂, ⚃, ⚄, ⚅ \}$을 생각하자. 일반적으로 주사위를 던져 눈을 관찰하는 경우의 확률론적 모델을 생각해보면 해당되는 확률함수

$p:\{ \{⚀\}, \{⚁\}, \{⚂\}, \{⚃\}, \{⚄\}, \{⚅\}, \{⚀, ⚁\}, \ldots, \{⚀, ⚁, ⚂, ⚃, ⚄, ⚅ \} \} \rightarrow [0,1]$

의 함수값은 다음과 같이 정의될 것이다:

$p(\{⚀\}) = 1/6, \\ p(\{⚁\}) = 1/6, \\ p(\{⚂\}) = 1/6, \\ p(\{⚃\}) = 1/6, \\ p(\{⚄\}) = 1/6, \\ p(\{⚅\}) = 1/6, \\ p(\{⚀, ⚁\}) = 1/3, \\ \cdots \\ p(\{⚁, ⚂, ⚃, ⚄, ⚅ \}) = 5/6, \\ p(\{⚀, ⚁, ⚂, ⚃, ⚄, ⚅ \}) = 1.$

즉, 각각의 표본에 대해 $1$보다 작은 어떤 숫자를 대응시킨 것이 확률함수이다.

우리는 주사위를 던지는 시행을 (충분히) 반복했을 때 각 사건이 일어날 “빈도”로 확률함수의 값을 해석한다. 물론 현실에서 주사위를 아무리 많이 던져도 정확히 확률함수가 지칭하는 빈도로 사건이 일어나지는 않겠지만, 충분히 공감가능한 한 기준을 제시해주는 것은 분명하다.

확률분포함수 (probability distribution function)

마음속에 있는 어떤 확률함수를 다른 이에게 제시하려면 표본공간에 있는 모든 표본에 대한 함숫값을 알려주면 된다. 표본의 총 개수가 $6$인 주사위 실험의 경우는 $2^6 = 64$개의 함숫값을 지정해주면 되었다. 확률함수의 함숫값의 총 갯수는 표본공간의 크기에 따라 기하급수적으로 증가함을 알 수 있다. 표본공간의 크기가 매우 큰 경우 이를 어떻게 다루는 것이 좋을까?

확률함수의 두 번째 성질인 덧셈 원리를 잘 이해하면 각 표본에 대한 함숫값을 정해주는 것만으로 충분하다는 사실을 알아낼 수 있다. 이런 관찰을 바탕으로 확률분포함수(probability distribution function)라는 것을 도입하게 된다.

$f_p : \Omega = \{⚀, ⚁, ⚂, ⚃, ⚄, ⚅ \} \rightarrow [0, 1],$ $\begin{aligned} f_p(⚀) &= 1/6, \\ f_p(⚁) &= 1/6, \\ f_p(⚂) &= 1/6, \\ f_p(⚃) &= 1/6, \\ f_p(⚄) &= 1/6, \\ f_p(⚅) &= 1/6. \\ \end{aligned}$

일반적으로 다음 두 가지 성질을 만족하는 함수를 확률분포함수라고 한다.

모든 $a \in \Omega$에 대해서 $0 \le f(a) \le 1$;
$\sum_{a \in \Omega} f(a) = 1$;

확률분포함수는 측도론의 관점에서는 확률질량함수(probability mass function)로 부르기도 한다. 확률함수의 두번째 성질인 덧셈 원리를 이용하면 다음이 성립함을 확인할 수 있다.

$p(A) = \sum_{a \in A} f_p(a).$

주사위 실험의 예를 들면,

$\begin{aligned} p(\{⚁, ⚂, ⚄ \}) &= \sum_{a \in \{⚁, ⚂, ⚄ \}} f_p(a) \\[10pt] &= f_p(⚁) + f_p(⚂) + f_p(⚄) \\[10pt] &= 1/6 + 1/6 + 1/6 \\ &= 1/2. \end{aligned}$

요약하자면, 확률분포함수는 확률함수의 모든 정보를 포함하면서도 보다 간결하게 제시할 수 있는 “경제성”을 가짐을 알 수 있다. 확률분포함수를 흔히 다음과 같은 테이블로 나타기도 한다.

$\square$	⚀	⚁	⚂	⚃	⚄	⚅
$f_p(\square)$	1/6	1/6	1/6	1/6	1/6	1/6

확률분포함수가 나타내는 정보를 한눈에 파악하기 가장 좋은 것은 아무래도 함수의 그래프를 통해서가 아닐까 싶다. 위의 확률 분포 함수를 그래프로 나타내면 다음과 같다.

Dice — 확률분포함수 (using: Desmos online calculator)

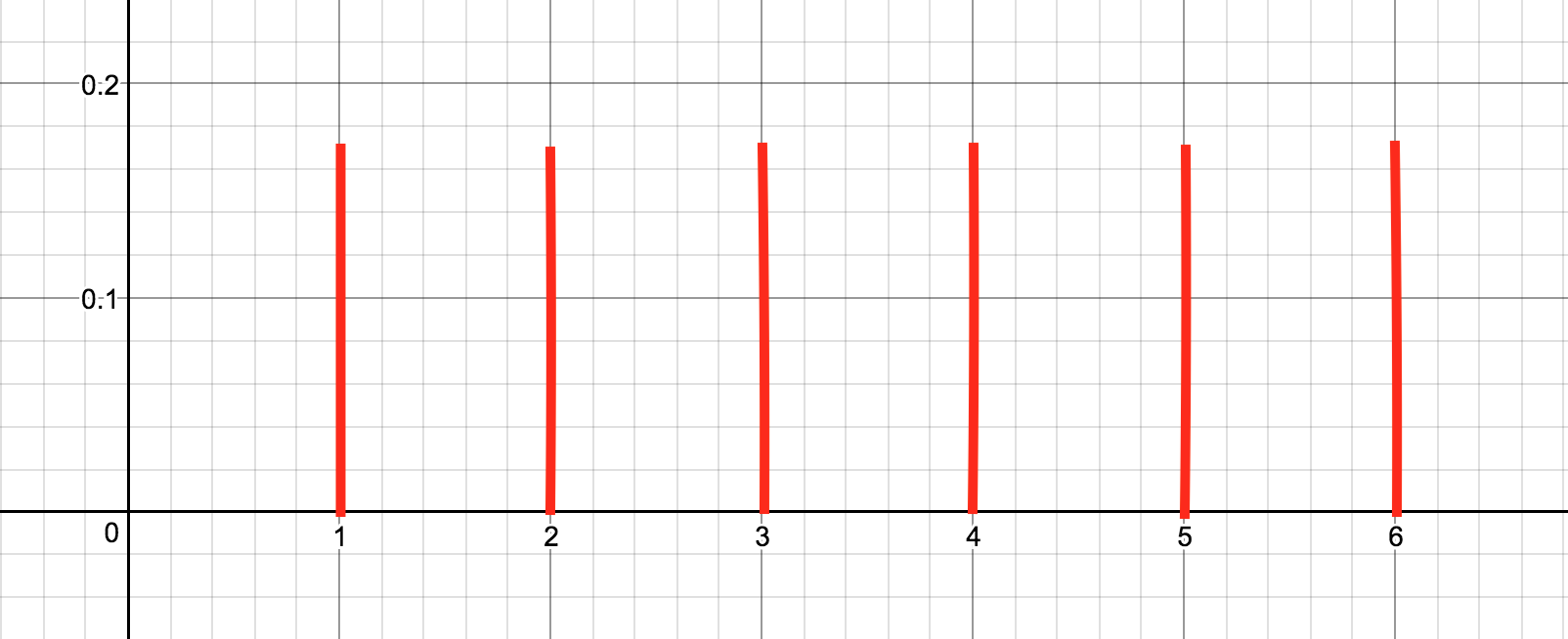
그래프를 보는 순간 당신의 머릿속에는 “분포”라는 단어가 스쳐지나갔을지도 모르겠다. 사실, “확률분포” 라고 하면 많은 사람들이 이런 그래프를 먼저 떠올리는 듯 하다. 필자의 생각에도 확률분포라는 개념은 확률분포함수의 그래프로 이해하는 것이 직관적이고 편안한 면이 있는 것 같다.

확률함수와 확률분포함수의 관계

확률함수와 확률분포함수 사이의 관계를 다시 한번 정리하고 넘어가자. 확률함수 $p : \mathscr{P}(\Omega) \rightarrow [0,1]$가 주어지면 이에 대응하는 확률분포함수 $f_p$를 정의할 수 있다:

$f_p : \Omega \rightarrow [0,1], \ f_p(a) = p(\{a\}).$

반대로, 확률분포함수 $f : \Omega \rightarrow [0,1]$가 주어지면 대응되는 확률함수 $p_f$를 정의할 수 있다:

$p_f : \mathscr{P}(\Omega) \rightarrow [0,1], \ p_f(A) = \sum_{a \in A} f(a).$

다음 내용으로 넘어가기 전에 이 상호관계가 무엇을 의미하는지 명확하게 정리해보기를 권한다.

확률변수의 등장

확률함수 혹은 확률분포함수가 주어진 후의 논리 전개 및 관련 계산은 많은 경우 확률변수라는 개념을 통해 이루어진다. 확률변수의 정의는 간단하다. 표본공간에서 실수로 가는 형태의 함수 $X: \Omega \rightarrow {\mathbb R}$라면 어떤 것이라도 확률변수(random variable)이다. 엄청나게 다양하고 무한히 많은 확률변수가 존재함을 알 수 있을 것이다. 곧 “이 많은 확률변수로 도대체 무얼 할까?” 하는 질문이 떠오를 수도 있는데, 대부분은 창고 속에 묻어두고 인간의 인지능력에 의미 있게 다가오는 한 줌의 확률변수만을 이용하게 된다.

앞에서의 주사위 실험과 관련하여 확률변수 $X$를 다음과 같이 정의하자.

$X : \Omega = \{⚀, ⚁, ⚂, ⚃, ⚄, ⚅ \} \rightarrow {\mathbb R}, \\ X(⚀) = 1, \\ X(⚁) = 2, \\ X(⚂) = 3, \\ X(⚃) = 4, \\ X(⚄) = 5, \\ X(⚅) = 6.$

확률변수 $X$가 의미하는 바를 알아챘는가? 그렇다. $X(\square)$는 $\square$가 보여주는 주사위 눈의 개수를 나타낸다. 이 $X$라는 확률변수를 이용하면 주사위 실험에서 일어나는 사건들을 간편하게 기술할 수 있다. 예를 들어 $[X = 1]$는 확률변수 $X$의 함수값이 1이 되게 하는 표본을 모두 모은 사건이다:

$[X = 1] = \{ a \in \Omega : X(a) = 1 \} = \{ ⚀ \}.$

그러면 $\{ ⚁, ⚂\}$는 $X$를 이용하여 어떻게 표현수 있을까? 그렇다. $\{ ⚁, ⚂\} = [X = 2, 3]$이 된다는 것을 금방 알아차렸을 것이다. 하지만 뭔가 대단한 것을 해낸 것 같지는 않다. 조금 더 “쓸모있을 지 모르는” 확률변수를 하나 정의해 보자.

$Y(⚀) = 1, \\ Y(⚁) = 0, \\ Y(⚂) = 1, \\ Y(⚃) = 0, \\ Y(⚄) = 1, \\ Y(⚅) = 0.$

그러면 $[Y = 1] = \{a \in \Omega : Y(a) = 1\} = \{ ⚀, ⚂, ⚄ \}$는 확률변수 $Y$에 대한 함숫값이 1인 표본들로 구성돤 사건이다. 한마디로 “홀수의 눈이 나오는 사건”임을 알 수 있다. 눈치 빠른 당신은

$[X = 1, 3, 5] = [Y = 1]$

임을 바로 알아챘을 지도 모르겠다. 아마도 확률변수 $X$와 $Y$ 사이에는 어떤 관계가 있는 것 같다.

또 하나의 확률변수를 더 생각해보자.

$\begin{aligned} Z(⚀) &= -1, \\ Z(⚁) &= 2, \\ Z(⚂) &= 1, \\ Z(⚃) &= 4, \\ Z(⚄) &= 3, \\ Z(⚅) &= 6. \end{aligned}$

어렵지 않게 $X-2Y = Z$가 됨을 확인 할 수 있을 것이다. 확률변수들 간에 연산을 할 수 있다는 것이다! (사실은 $Z$를 $X - 2Y$의 함수값으로 정의했다.)

확률변수로 할 수 있는 일 : 기댓값과 분산의 정의

확률론과 관련하여 “기댓값”과 “분산”이라는 개념이 이미 익숙하게 느껴질텐데, 사실 확률변수라는 개념을 도입하기 전에는 정의조차 할 수 없는 것들이다. 기댓값과 분산은 확률분포가 아니라 확률변수의 특성을 나타내는 값들이기 때문이다. 따라서 기댓값을 나타내는 표현 $E[X]$에는 확률변수 $X$가 포함되는 것이 매우 자연스럽다.

확률함수 $p : \Omega \rightarrow [0, 1]$가 주어지고 이에 기반을 두는 확률변수 $X : \Omega \rightarrow {\mathbb R}$가 주어지면 $X$에 대한 기댓값(expectation)을 다음과 같이 정의한다.

$E[X] = \sum_{a \in \Omega} p(a)X(a).$

여기서 “기반을 둔다”는 것은 단순히 함수 $p$와 $X$의 정의구역이 $\Omega$로 일치한다는 뜻이다.

주사위 실험의 예로 돌아가서 $X$에 대한 기댓값을 구해보면 다음과 같다.

$\begin{aligned} E[X] =& \sum_{a \in \{⚀, ⚁, ⚂, ⚃, ⚄, ⚅ \}} p(a)X(a) \\ =& p(⚀)X(⚀) + p(⚁)X(⚁) + p(⚂)X(⚂) \\ & + p(⚃)X(⚃) + p(⚄)X(⚄) + p(⚅)X(⚅) \\ =& 1/6\cdot 1 + 1/6\cdot 2 + 1/6\cdot 3 + 1/6\cdot 4 + 1/6\cdot 5 + 1/6\cdot 6 \\ =& 21/6. \end{aligned}$

앞에서 확률변수들 간에 연산을 할 수 있다는 사실을 보았다. 예를 들면 $X, Y$라는 확률변수에 연산을 적용하여 또다른 확률변수 $X + Y$와 $aX$를 얻를 수 있다. (여기서 $a \in {\mathbb R}$은 상수이다.) 새로 얻어진 확률변수들에 대한 기댓값을 구해보면 기존 $X, Y$에 대한 기댓값과 다음의 관계를 가진다.

$\begin{aligned} E(X + Y) &= E(X) + E(Y) \\ E(aX) &= aE(X). \end{aligned}$

이것을 기댓값의 선형성(linearity)이라고 한다. 이 성질을 이용하면 $X, Y$의 기댓값으로 부터 $X + Y$의 기댓값을 구할 수 있다.

확률변수에 관련된 또 하나의 값, 분산(variance)을 정의해보자.

$\begin{aligned} V[X] = E[(X - E(X))^2]. \end{aligned}$

기댓값의 선형성을 이용하면 분산을 다음과 같이 계산할 수 있다.

$\begin{aligned} V[X] &= E[(X - E[X])^2] \\ &= E[X^2 - 2E[X]X + E[X]^2] \\ &= E[X^2] - 2E[X]E[X] + E[X]^2 \\ &= E[X^2] - E[X]^2. \end{aligned}$

보다 일반적으로 함수 $F: \mathbb{R} \rightarrow \mathbb{R}$에 대해 $F(X)$라는 새로운 확률변수를 정의할 수 있다:

$F(X) : \Omega \rightarrow \mathbb{R}, \ F(X)(a) = F(X(a)).$

즉, $F(X)$는 $F$와 $X$라는 두 함수의 합성함수이다. 예를 들어, $F(x) = x^3 -x +1$이면 $F(X) = X^3 - X +1$이고

$E[F(X)] = E[X^3 -X + 1] = \sum_{a \in \Omega} p(a)\cdot (X(a)^3 - X(a) +1)$

이 된다.

확률변수는 자신만의 확률분포를 재조직한다

확률함수 $p$ 혹은 그에 대응되는 확률분포함수 $f$에 기반을 둔 확률변수 $X$를 생각하자. 확률함수와 확률분포함수가 본질에서 같은 정보의 두 가지 다른 표현이라는 것을 상기하면 두 함수가 다음의 관계를 만족함을 알 수 있다.

$\begin{aligned} p &= p_f \\ f &= f_p \end{aligned}$

확률변수 $X$는 자신만의 새로운 확률함수와 확률분포함수를 정의하게 되는데 그 과정을 엄밀하게 살펴보자. $X$의 확률분포함수 $f_X : \Omega_X \rightarrow [0,1]$의 정의구역, 즉 표본공간은 $\Omega_X = \{X(a) : a \in \Omega\} \subset \mathbb{R}$이고 다음과 같이 정의된다:

$\color{red}{f_X(\alpha)} = \color{red}{p[X=\alpha]} = \sum_{a \in [X=\alpha]}f(a) = \color{red}{\sum_{X(a) = \alpha}f(a)}.$

이 관계를 잘 기억해두도록 하자. 확률분포함수와 확률함수의 관계를 이용하면 $\mathcal{A} \subset \Omega_X$에 대해서

$p_X(\mathcal{A}) = \sum_{\alpha \in \mathcal{A}}f_X(\alpha)$

임을 알 수 있다. 그렇다면 다음의 $\mathcal{A} = \{\alpha\}$인 경우 확률을 기존의 확률함수 $p$를 이용하여 기술하면 어떻게 될까?

$p_X(\{\alpha\}).$

정의를 이용하면

$\begin{aligned} p_X(\{\alpha\}) = \sum_{\alpha' \in \{\alpha\}} f_X(\alpha') = f_X(\alpha) = p[X=\alpha] \end{aligned}$

이 됨을 어렵지 않게 알 수 있다.

앞서 정의한 확률변수 $X, Y$로 예를 들면 다음과 같다.

$f_X : \Omega_X = \{1, 2, 3, 4, 5, 6\} \rightarrow [0,1] \\ f_X(1) = 1/6 \\ f_X(2) = 1/6 \\ f_X(3) = 1/6 \\ f_X(4) = 1/6 \\ f_X(5) = 1/6 \\ f_X(6) = 1/6.$ $f_Y : \Omega_Y = \{0, 1\} \rightarrow [0,1] \\ f_Y(0) = 1/2 \\ f_Y(1) = 1/2.$

$ $

참고자료

[1] A. Shirayaev (translator: D. Chibisov), Probability- 1, third edition (2016), Springer.
[2] 김민형, 확률론의 선과 악: 2. 확률론의 기원 (네이버티비 동영상).
[3] Mathematical monk, Probability primer (유튜브 동영상).
[4] PennStae, Eberly College of Science, STAT 414: Probability theory (온라인 코스).

읽으시다 오류나 부정확한 내용을 발견하시면 꼭 알려주시길 부탁드립니다. 감사합니다.
(권 경모님, 권 휘님, 박 진우님, 손 주형님, 이 규복님, 김 기철님 감사드립니다.)