열 개의 팔을 가진 강도

“카지노에 가본 적이 있으신가요?” 이 질문에 “그렇습니다!” 하고 답할 사람은 많지 않을 것 같지만 “카지노 로열” 같은 영화를 본 경험이 있다면 카지노 풍경을 상상하는 것은 그리 어렵지 않을 것이다.

슬롯머신을 머릿속에 그려보자. 먼저 제일 간단한 경우로, 레버를 당기면 (실제로 그럴 리는 없지만) 항상 같은 금액이 나온다고 가정해보자. 이런 경우 슬롯머신의 reward(보상) 분포가 deterministic 하다고 말한다. 레버를 당기기 전에 이미 어떤 금액이 나올지 결정되어 있다는 뜻이다. 이런 경우 한 번만 당겨보면 이 슬롯머신에 대해 필요한 모든 정보를 아는 샘이 된다. 당연히 카지노 측에서 이렇게 만들어 놓을 리가 없다. 실제로는 어떤 확률 분포를 정하고 거기에 맞추어 보상이 결정되도록 프로그램되어 있을 것이다.

슬롯머신의 레버를 당기면 기댓값이 0이고 분산이 1인 정규분포(Gaussian distribution, normal distribution)에 따라 숫자를 토해내는 이상적인 상황을 생각해보자. 여기서 평균이 0인 분포를 따른다는 것은, 이 슬롯머신의 레버를 당기는 시행을 반복하면서 얻게 되는 수치들의 평균을 계산해보면 그 시행 횟수가 많아질수록 점점 0에 가까워지리라는 것이라는 것을 뜻한다.

한편, 분산은 주어진 분포에 따라 수치를 추출하는 시행을 반복할 때 기댓값에 가까운 값이 나올 가능성과 관계가 있다. 예를 들어 아래 그림으로 표현된 두 분포에 따라 수치를 출력해보면 분산이 상대적으로 작은 왼쪽 분포(분산 0.9)의 경우 평균인 0에 가까운 값이 자주 출력되는 반면, 분산이 큰 오른쪽 분포(분산 2.5)의 경우 평균에서 먼 값들도 유사한 빈도로 출력된다.

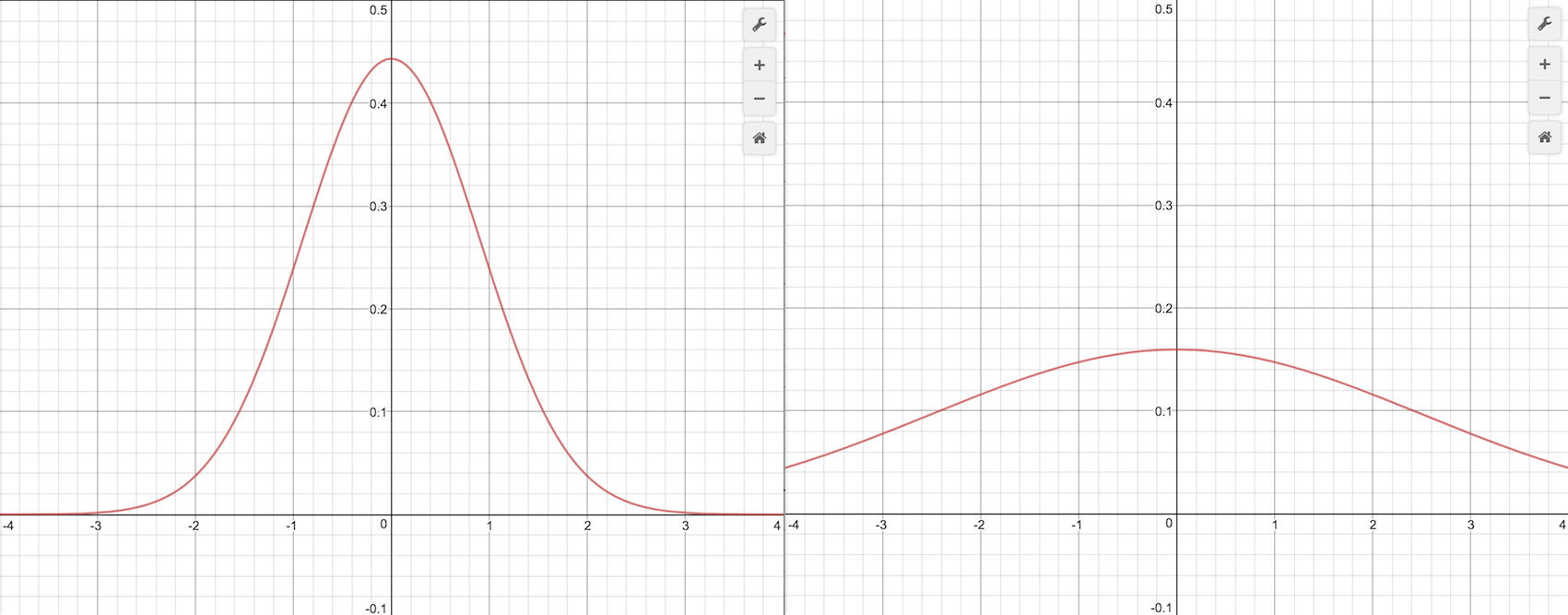
또 한가지 생각해볼 수 있는 것은, 분산이 작은 경우 반복 시행의 평균을 통해 상대적으로 빠르게 기댓값에 접근해갈 것이라는 사실이다. (물론 분산이 큰 경우에도 상대적으로 속도는 느리겠지만 어쨌든 기댓값에 접근해간다.) 이 원리를 이용하면, 슬롯머신이 정규분포를 따르지만 그 기댓값이 알려져있지 않은 경우에도 여러 번의 반복 시행을 통해서 그 분포의 기댓값이 얼마인지를 추정해갈 수 있다. 극단적인 경우로 분산이 0인 다음 그림의 분포는 “항상” 그리고 “반드시” 기댓값인 0을 출력하게 된다.

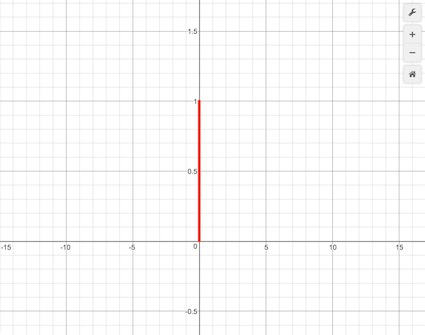
열 개의 팔을 가진 강도

Multi-armed bandit. 팔 여러 개 달린 강도란 뜻이다. 카지노의 슬롯머신을 가리켜 one-armed bandit, 즉 “팔 하나 달린 강도”라고 부르는 데서 유래한 용어로, “사실상” 돈을 강탈해간다는 의미에서 그러하다.

이제 1부터 10까지 번호가 붙여진 열 개의 슬롯머신이 놓여있는 방을 머릿속에 떠올려보자. 기댓값이 0이고 분산이 1인 표준정규분포에 따라 숫자 열 개를 추출하자: $m_1, m_2, \ldots, m_{10}$. 각 슬롯머신의 reward 분포는 기댓값이 $m_i$이고 분산이 1인 정규분포에 따르도록 설정이 된다. 아래 그림에 reward 분포가 도식화되어 있는데 (조금 후에 설명할 어떤 이유로) 그림에서는 $i$번째 머신의 기댓값 $m_i$가 $q_*(i)$로 표시되어 있다.

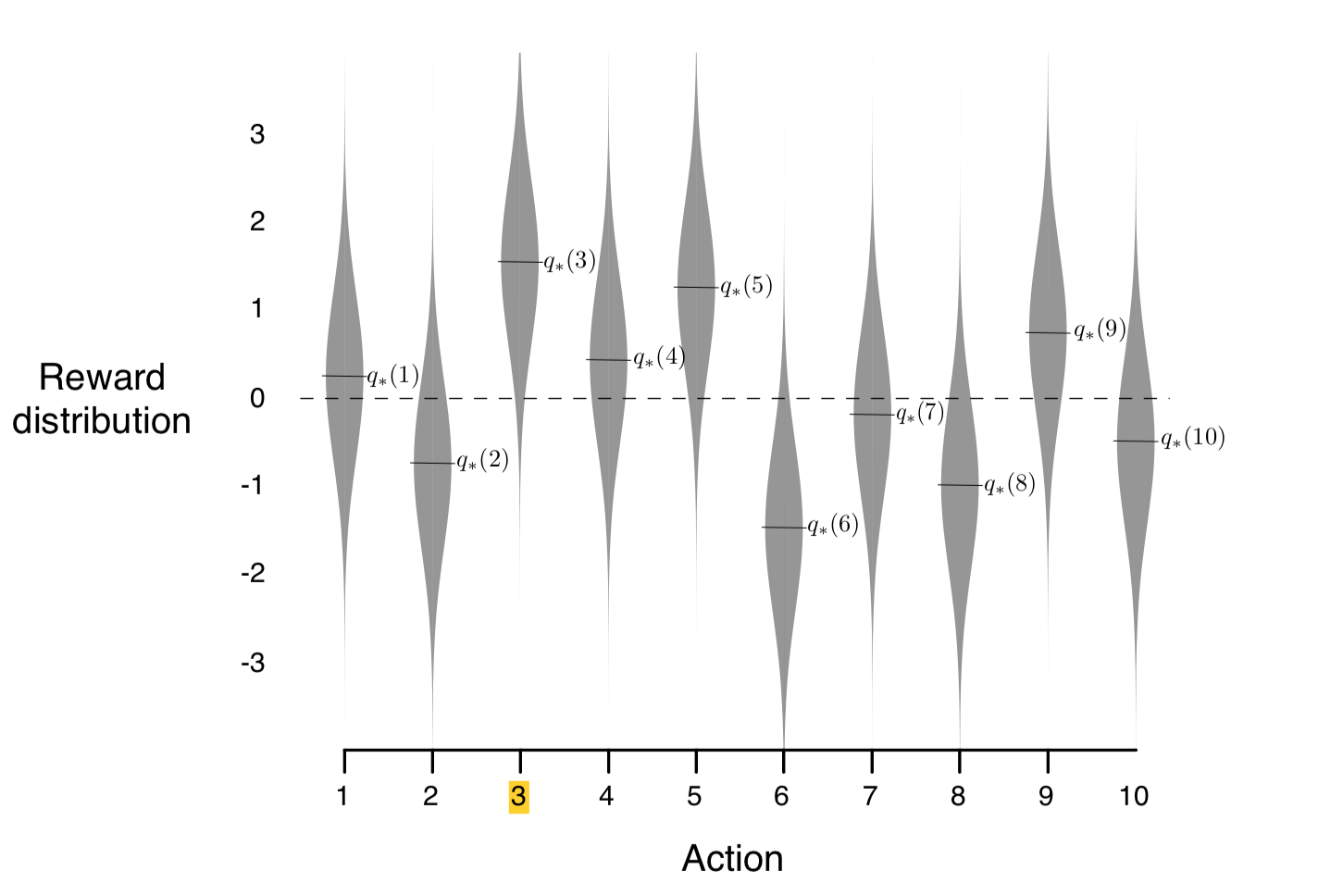
Multi-armed bandit (여기서는 구체적으로 10-armed bandit) 문제는 슬롯머신들의 reward distribution을 모르는 상태에서 선택한 하나의 슬롯머신의 “팔”을 당겨 해당 reward를 얻는 시행을 충분히 많은 횟수로 반복하면서 얻게 되는 reward의 총합을 최대화하는 문제다. 이 문제를 풀어나가기 위해 수많은 횟수의 시행을 반복하는 힘든 임무를 대신해 줄 주인공을 agent라 부르자. Agent가 각 시점(time step)에 열 개 중 하나의 슬롯머신을 “선택”하여 레버를 당기는 행위를 그 시점에서의 action이라 한다. 선택적 요소가 포함되면서 agent가 어떤 action을 취했을 때 얼만큼의 reward가 주어질 것인지에 대한 “가능성”을 평가 (evaluation) 해나가야 하고 그에 따라 어떤 패턴으로 행동해나가야 하는지 전략을 세워야 한다. 이 전략을 구체적으로 표현한 함수를 policy라 부른다. 우리말로는 “정책” 정도로 부를 수 있을 것이다. 시점 $t$에서 agent가 취하는 action을 $A_t$, 그로 인해 얻게 되는 reward를 $R_t$로 부르기로 하자.

Action의 가치를 어떻게 평가할 것인가

열 개의 슬롯머신들의 reward 분포가 그림 3처럼 주어졌다고 하자. 먼저 각 머신들의 reward 분포를 전부 알아버린 상황이라고 하면 우리는 agent가 어떤 선택을 하도록 해야 할까? 그렇다. 당연히 3번 슬롯머신의 팔만 계속 당기도록 해야 할 것이다. 3번을 선택하는 시행을 반복할수록 reward의 누적합의 평균은 그 기댓값인 1.5에 가까워져 갈 것임에 비해 다른 아홉 개 머신들의 경우 그보다 작은 값으로 수렴해갈 것이기 때문이다. 그러면 이 문제를 해결하는 열쇠는 가장 큰 기댓값의 reward 분포를 가지는 슬롯머신이 3번이라는 것을 최대한 빨리 알아내는 일일 것이다. 즉, 3번 슬롯머신을 선택하는 action의 가치(value)가 가장 높다는 것을 파악하는 것이 문제의 핵심이다. Reward 분포를 모르는 상태에서 어떻게 이것이 가능할까?

우리가 agent를 통해 할 수 있는 일이란 각 시점 $t$에 하나의 action $A_t$를 취해서 그에 따르는 reward $R_t$를 받아 확인하는 것이 전부라는 것을 상기하자. 그렇다면 슬롯머신들의 reward 분포를 알아내기 위해 제일 먼저 해야 할 일은 일단 아무 슬롯머신 혹은 마음에 드는 번호의 머신을 골라 당겨보는 일일 것이다. 그로 인해 받게 되는 reward 값이 해당 분포의 기댓값과 얼마나 일치할지를 알 수는 없지만 그래도 어느 정도 가까운 값일 거라고 기대해 볼 수는 있다.

각 action의 가치를 평가하고 점점 더 정확해지도록 업데이트해나가기 위해 가치함수(action-value function) $Q_t(a)$를 도입하자. $t$와 $a$에 대한 함숫값인 $Q_t(a)$는 $t$ 시점에서 $a$라는 action의 가치를 수치화한 것으로 생각하면 되겠다. 즉 수치가 클수록 $t$라는 시점에 $a$라는 action이 선택할 가치가 높다고 예상한다는 의미다. 한편 우리가 모든 슬롯머신의 reward 분포를 알았다고 가정했을 때 각 action에 부여할 만한 가치에 대해 생각해보자. 잠시 생각을 해보면 reward 분포의 기댓값이 높을수록 해당 action을 취하는 것이 더 높은 가치를 가진다는 것을 알 수 있을 것이다. 따라서 각 action $a$의 진정한 가치, 혹은 목표가치를 $q_{* }(a)=m_a$로 정의하는 것은 그리 이상한 일은 아니다.

가치함수 $Q_t(a)$를 구체적으로 정의해보자. 한 가지 자연스러운 선택은 $a$라는 action을 취하여 받은 reward의 평균을 그 함숫값으로 정하는 것이다: $t$ 시점 이전까지 $a$를 선택한 횟수를 $N$, 그때까지 $a$를 선택하여 얻은 reward의 총합을 $M$이라고 할 때, 시점 $t$에서의 $a$라는 action의 가치를

라고 정의하자. $t$라는 시점에 도달하기까지 평균적으로 reward를 많이 얻게하는 action일수록 가치가 높아진다는 것을 바로 알 수 있을 것이다.

Exploitation vs. Exploration

여태까지의 논의를 요약해보면, 10-armed bandit 문제를 해결하는 핵심은 가장 큰 가치 $q_{* }(a)$를 가지는 action $a$에 해당하는 슬롯머신을 최대한 빨리 알아내는 것이다. 그 이후에는 오로지 $a$라는 action만 반복해서 취하면 장기적으로 reward의 총합을 최대화할 수 있을 것이다. 일반적으로, 현재의 정보로만 판단할 때 최대 가치를 가지는 action”만”을 선택해나가는 전략을 exploitation이라고 하고 그러한 개별 action을 greedy action이라고 한다. 진정한 의미의 최대 가치를 가지는 action을 알아낸 경우에는 당연히 greedy action을 취해야 함은 물론이지만, greedy action만을 선택하는 것은 상황에 따라서는 눈앞의 이익만 좇는 탐욕스러운 행동으로 전락해버릴 수도 있다. 그러면 아직 최적의 action을 판단하기에 충분한 정보를 얻지 못한 상황에서 각 머신들의 reward 분포에 대한 정보를 알아가기 위해서 어떤 전략을 취해야 할까?

이제부터 agent에 전략을 어떻게 프로그래밍할 것인지 구체적으로 생각해보도록 하자. 우리가 agent에게 설정해야 할 프로그램의 내용은 각 시점 $t$에서 몇 번 슬롯머신을 선택할지 (확률적으로) 정해주는 것이다. 수학적으로는 시점 $t$에 대한 함수 $A_{t}: \{ 0, 1, 2, \ldots \} \rightarrow \{ 1, 2, \ldots ,10 \}$를 정의하는 것이다. (좀 더 엄밀하게는 $A_t$를 확률변수로 정의해야 한다.) 예를 들어 $A_0 = 7$로 프로그래밍을 한다면 agent는 최초에 일곱 번째 슬롯머신을 선택할 것이다. 만일 우리가 모든 $t$에 대해 일일이 $A_t$의 값을 정해준다면 아마 agent가 훌륭한 퍼포먼스를 보여주기 힘들 거라고 쉽게 예상할 수 있을 것이다. 실제 문제 상황에서는 agent에게는 물론 우리에게도 슬롯머신들의 reward 분포가 알려져 있지 않기 때문이다. 이 지점이 기계학습, 더 나아가 강화학습의 유용성이 빛을 발하는 지점인데, 그 포인트는 agent가 최대한 greedy action을 취하면서도 가치함수 $Q_t$를 잘 업데이트해나갈 수 있도록 $A_t$ 함수를 만들어 가는 것이다. 이처럼 현재의 greedy action에 만족하지 않고 더 나은 가치를 가지는 action이 없는지 다른 슬롯머신들을 탐색해보는 전략을 exploration이라고 한다.

$\varepsilon$-greedy 알고리즘

$\varepsilon$-greedy 알고리즘은 정해진 (작은) 양수 $\varepsilon$에 대해 $1-\varepsilon$의 확률로 greedy action을 취하고 나머지 $\varepsilon$의 확률로 greedy action 이외의 action을 임의로 선택하는 알고리즘이다. $1-\varepsilon$의 확률로 최대한 많은 reward를 긁어모으면서 (exploitation) 작은 $\varepsilon$ 확률로 더 가치 있는 action이 있는지 탐색하는 (exploration) 전략이다.

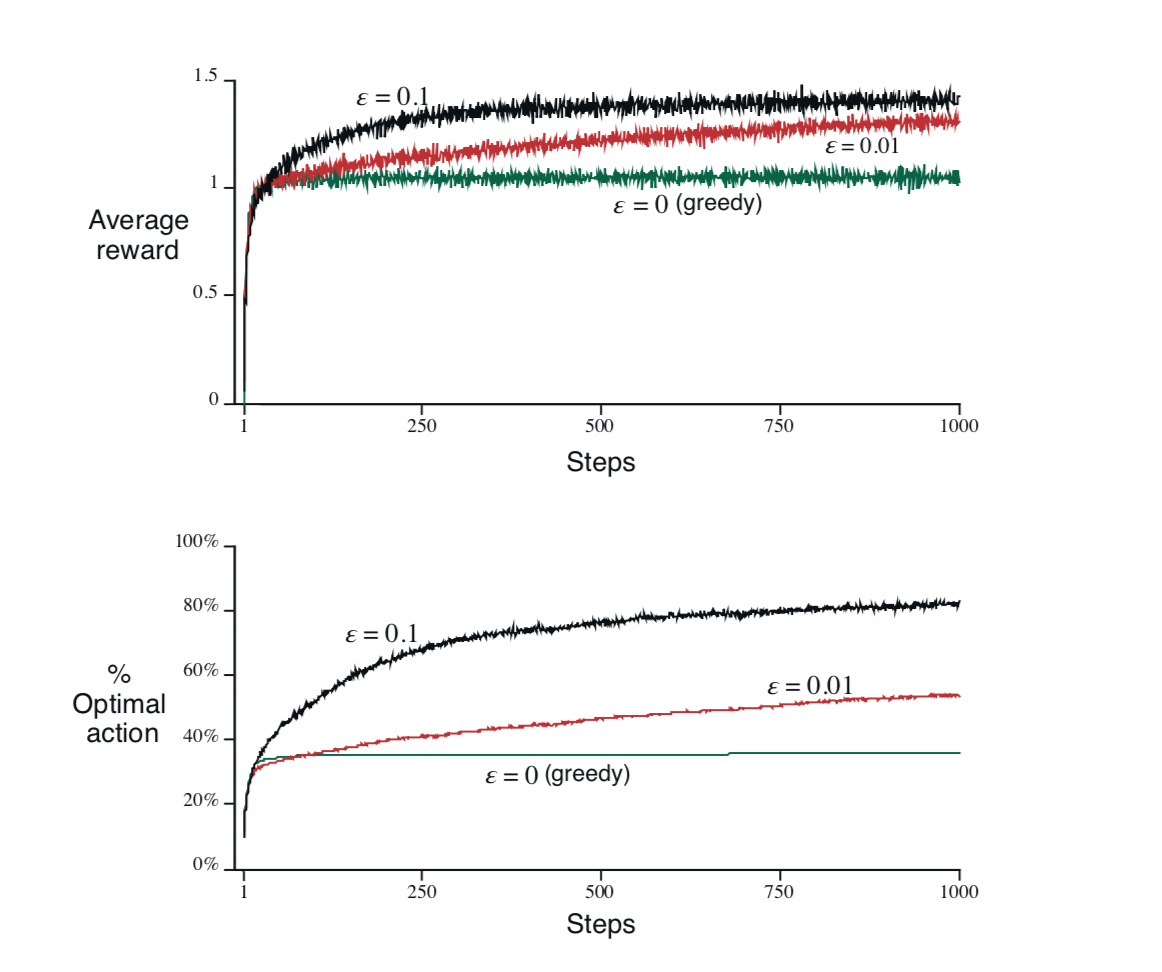
그림 4는 $\varepsilon$의 크기에 따른 $\varepsilon$-greedy 알고리즘의 퍼포먼스를 서로 비교하여 그래프로 나타낸 것이다. 구체적으로, 임의의 10-armed bandit 2000개를 생성한 후 $0.1$-greedy, $0.01$-greedy 그리고 $0$-greedy 알고리즘으로 각각 1000회의 time step 동안 action을 선택하도록 한 결과의 평균이 그래프로 표시되어 있다.

위쪽 그래프는 선택 횟수의 증가에 따른 누적 reward의 평균을 나타낸다. 먼저 눈에 띄는 것이, 어떤 알고리즘을 이용하든 간에 action 횟수의 증가에 따라 누적된 reward의 평균이 증가하고 일정 시점이 지나면 안정화됨을 알 수 있다. $0$-greedy 알고리즘(보통은 그냥 greedy 알고리즘으로 부른다)이 다른 두 알고리즘보다 시작 직후 아주 잠깐 빠른 진전을 보이지만 결국 더 낮은 값에서 안정화된다. 최초의 정보에만 의존해 전혀 탐색하지 않고 눈앞의 이익만 좇은 결과이다.

아래쪽 그래프는 각 알고리즘이 최적의 action을 선택한 빈도를 백분율로 나타내고 있다. 시작한 지 얼마 되지 않은 시점부터 열 번 중에 한 번 정도 탐색을 한 $0.1$-greedy 알고리즘이, 백번에 한 번 탐색을 하는 $0.01$-greedy 알고리즘과 탐색을 전혀 하지 않는 greedy 알고리즘보다 압도적으로 높은 비율로 최적의 action을 선택하기 시작하여 그 빈도가 80%에까지 이른다. Greedy 알고리즘은 40%가 채 안 되는 곳에 머무르지만, 상대적으로 미미한 횟수의 탐색이라도 주기적으로 시행하는 $0.01$-greedy 알고리즘은 서서히 진전을 보여 50% 근처까지 도달한다. 한 가지 재미있는 점은 time step을 1000회 이상으로 늘여가면 $0.01$-greedy 알고리즘이 $0.1$-greedy 알고리즘을 서서히 추월하여 결국 두 그래프에서 모두 제일 나은 퍼포먼스를 보일 것이라는 사실이다. 이를 고려하여 시작은 $0.1$-greedy 알고리즘으로 하되 어느 시점부터 점점 $\varepsilon$의 크기를 줄여나가는 알고리즘을 생각해볼 수도 있다.

일반화된 강화학습 문제

Multi-armed bandit (MAB) 문제는 강화학습 문제 중에서도 한가지 요소가 극도로 단순화된 형태로 이를 nonassociative라는 형용사로 표현한다. Associate가 “연결하다” 혹은 “연상시키다”라는 의미를 가지는 동사인데, 더욱 일반적인 강화학습 문제에서는 state라는 요소가 도입되어 시간이 지남에 따라 agent의 action에 따라 state가 변화되는 가능성이 포함되어있다. 각 state마다 agent가 취할 수 있는 action의 선택사양이 달라지기도 한다. 이렇게 더욱 복잡해지고 일반화된 형태의 강화학습 문제를 associative하다고 표현한다. MAB 문제와 관련하여 예를 든다면 몇 번 슬롯머신을 선택하느냐에 따라 새로운 방으로 이동하여 슬롯머신이 아닌 다른 게임에 대한 action을 취하고 그로 인해 또 다른 방으로 이동하게 되고 … 이런 식으로 계속 진행된다.

일반화된 강화학습의 개념은 agent와 environment, 그리고 action, state, reward, policy라는 주요소들이 포함된 형태로 정의되는데 수학적으로는 MDP (Markov Decision Process)라는 모델로 기술된다.

참고문헌

1. R. Sutton, A. Barto, Reinforcement leaning: an introduction, second edition (final draft).

읽으시다 오류나 부정확한 내용을 발견하시면 꼭 알려주시길 부탁드립니다. 감사합니다.
(권 경모님, 권 휘님, 박 진우님 감사드립니다.)